Question

【题目】如图，点A、B在直线l上，AB=10cm，⊙B的半径为1cm，点C在直线l上，过点C作直线CD且∠DCB=30°，直线CD从A点出发以每秒4cm的速度自左向右平行运动，与此同时，⊙B的半径也不断增大，其半径r（cm）与时间t（秒）之间的关系式为r=1+t（t≥0），当直线CD出发多少秒直线CD恰好与⊙B相切．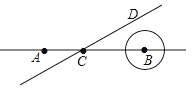

Answer 1

【答案】解：当直线与圆相切时，点C在圆的左侧，
∵∠DCB=30°，直线CD与⊙B相切，
∴2DB=BC，
即2（1+t）=10-4t，
解得：t=
当直线与圆相切时，点C在圆的右侧，
∵∠DCB=30°，直线CD与⊙B相切，
∴2DB=BC，
即2（1+t）=4t-10，
解得：t=6，
故答案为： 或6．
【解析】 根据直线与圆相切和勾股定理，圆的半径与BC的关系，注意有2种情况解答即可．