ΧβΡΩΡΎ»ί
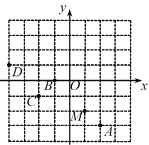
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ“Μ¥ΈΚ· ΐyΘΫ©¹x”κΕΰ¥ΈΚ· ΐyΘΫ©¹x2+bx+cΒΡΆΦœσœύΫΜ”Ύ‘≠ΒψOΚΆΝμ“ΜΒψAΘ®4Θ§©¹4Θ©Θ°
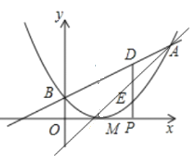
Θ®1Θ©«σΕΰ¥ΈΚ· ΐ±μ¥ο ΫΘΜ
Θ®2Θ©÷±œΏxΘΫmΚΆxΘΫm+2Ζ÷±πΫΜœΏΕΈAO”ΎCΓΔDΘ§ΫΜΕΰ¥ΈΚ· ΐyΘΫ©¹x2+bx+cΒΡΆΦœσ”ΎΒψEΓΔFΘ§Β±mΈΣΚΈ÷Β ±Θ§ΥΡ±Ώ–ΈCEFD «ΤΫ––ΥΡ±Ώ–ΈΘΜ
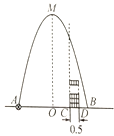
Θ®3Θ©‘ΎΒΎΘ®2Θ©ΧβΒΡΧθΦΰœ¬Θ§…ηCE”κx÷αΒΡΫΜΒψΈΣMΘ§ΫΪΓςCOM»ΤΒψOΡφ ±’κ–ΐΉΣΒΟΒΫΓςCΓδOMΓδΘ§Β±CΓδΓΔMΓδΓΔF»ΐΒψΒΎ“Μ¥ΈΙ≤œΏ ±Θ§«κΜ≠≥ωΆΦ–Έ≤Δ÷±Ϋ”–¥≥ωΒψCΓδΒΡΉίΉχ±ξΘ°
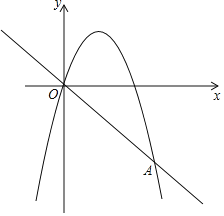
ΓΨ¥πΑΗΓΩΘ®1Θ©yΘΫ©¹x2+3xΘΜΘ®2Θ©Β±mΈΣ1 ±Θ§ΥΡ±Ώ–ΈCEFD «ΤΫ––ΥΡ±Ώ–ΈΘΜΘ®3Θ©ΆΦœξΦϊΫβΈωΘ§CΓδΘ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©Α―Θ®0Θ§0Θ©Θ§AΘ®4Θ§©¹4Θ©¥ζ»κyΘΫ-x2+bx+cΘ§Φ¥Ω…«σΫβΘΜ
Θ®2Θ©…ηCΘ®mΘ§©¹mΘ©Θ§DΘ®m+2Θ§©¹m©¹2Θ©Θ§±μ Ψ≥ωEΘ§FΉχ±ξΘ§ΗυΨίCEΓΈDFΘ§Ω…ΒΟΒ±CEΘΫDF ±Θ§ΥΡ±Ώ–ΈCEFDΈΣΤΫ––ΥΡ±Ώ–ΈΘ§Φ¥©¹m2+3m+mΘΫ©¹m2©¹m+2+m+2Θ§Φ¥Ω…«σΫβΘΜ
Θ®3Θ©ΉςCΓδHΓΆx÷α”ΎHΘ§Ω…÷ΛΓςFHCΓδΓΉΓςFMΓδOΘ§‘ρ![]() Θ§Φ¥
Θ§Φ¥![]() Θ§Φ¥Ω…«σΫβΘ°
Θ§Φ¥Ω…«σΫβΘ°
ΫβΘΚΘ®1Θ©Α―Θ®0Θ§0Θ©Θ§AΘ®4Θ§-4Θ©¥ζ»κyΘΫ©¹x2+bx+cΒΟ![]() Θ§
Θ§
ΫβΒΟΘΚ![]() Θ§
Θ§
Ι ≈ΉΈοœΏΒΡ±μ¥ο ΫΈΣΘΚyΘΫ©¹x2+3xΘΜ
Θ®2Θ©…ηCΘ®mΘ§©¹mΘ©Θ§DΘ®m+2Θ§©¹m©¹2Θ©Θ§
‘ρEΘ®mΘ§©¹m2+3mΘ©Θ§F[m+2Θ§©¹Θ®m+2Θ©2+3Θ®m+2Θ©]Θ§Φ¥FΘ®m+2Θ§©¹m2©¹m+2Θ©Θ§
ÿCEøDFȧ
ΓύΒ±CEΘΫDF ±Θ§ΥΡ±Ώ–ΈCEFDΈΣΤΫ––ΥΡ±Ώ–ΈΘ§
Φ¥©¹m2+3m+mΘΫ©¹m2©¹m+2+m+2Θ§
ΫβΒΟmΘΫ1Θ§
Φ¥Β±mΈΣ1 ±Θ§ΥΡ±Ώ–ΈCEFD «ΤΫ––ΥΡ±Ώ–ΈΘΜ
Θ®3Θ©Μ≠ΆΦ»γœ¬Θ§ΉςCΓδHΓΆx÷α”ΎHΘ§
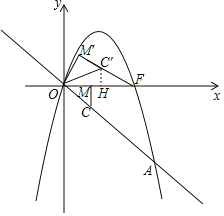
Β±mΘΫ1 ±Θ§CΘ®1Θ§-1Θ©Θ§DΘ®3Θ§-3Θ©Θ§FΘ®3Θ§0Θ©Θ§Φ¥FΒψΈΣ≈ΉΈοœΏ”κx÷αΒΡ“ΜΗωΫΜΒψΘ§
ΓύOMΘΫCMΘΫ1Θ§OCΘΫ![]() Θ§
Θ§
ΓΏΓςCOM»ΤΒψOΡφ ±’κ–ΐΉΣΒΟΒΫΓςCΓδOMΓδΘ§
ΓύOMΓδΘΫCΓδMΓδΘΫ1Θ§ΓœOMΓδCΓδΘΫΓœOMCΘΫ90ΓψΘ§
‘ΎRtΓςOMΓδF÷–Θ§FMΓδΘΫ![]() ΘΫ2
ΘΫ2![]() Θ§
Θ§
ΓύFCΓδΘΫ2![]() ©¹1Θ§
©¹1Θ§
ΓΏΓœCΓδFHΘΫOFMΓδΘ§
ΓύΓςFHCΓδΓΉΓςFMΓδOΘ§
Γύ![]() Θ§Φ¥
Θ§Φ¥![]() Θ§
Θ§
ΓύFHΘΫ![]() Θ§CΓδHΘΫ
Θ§CΓδHΘΫ![]() Θ§
Θ§
ΓύOHΘΫOF©¹FHΘΫ![]() Θ§
Θ§
ΓύCΓδΘ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°

 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ