题目内容
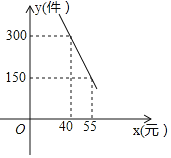
【题目】大学毕业生小王响应国家“自主创业”的号召，利用银行小额无息贷款开办了一家饰品店．该店购进一种今年新上市的饰品进行销售，饰品的进价为每件40元，售价为每件60元时，每月可卖出300件．市场调查反映：调整价格时，售价每涨1元每月要少卖10件；售价每下降1元每月要多卖20件．为了获得更大的利润，现将饰品售价调整为x（元/件），每月饰品销量为y（件），月利润为w（元）．
（1）直接写出y与x之间的函数关系式；
（2）如何确定售价才能使月利润最大？求最大月利润；
（3）为了使每月利润不少于6000元应如何控制售价？
【答案】（1）
；
（2）当售价为65元时，利润最大，最大利润为6250元；
（3）将销售价格控制在55元到70元之间（含55元和70元）才能使每月利润不少于6000元.
【解析】
（1）直接根据题意售价每涨1元每月要少卖10件；售价每下降1元每月要多卖20件，进而得出等量关系；
（2）利用每件利润×销量=总利润，进而利用配方法求出即可；
（3）利用函数图象结合一元二次方程的解法得出符合题意的答案．
（1）由题意得：涨价时：y=300-（x-60）×10=-10x+900，
降价时：y=300+(60-x) ×20=-20x+1500，
即
（2）由题意可得：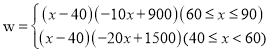
，
化简得：
，
即
，
6125＜6250，
故当售价为65元时，利润最大，最大利润为6250元；
（3）令w=6000，
即6000=﹣10（x﹣65）2+6250，6000=﹣20（x-57.5）2+6125，
解得：x1=55，x2=60，x3=70，
当w≥6000时，
知：55≤x≤70，
故将销售价格控制在55元到70元之间（含55元和70元）才能使每月利润不少于6000元．
练习册系列答案
相关题目
