Question

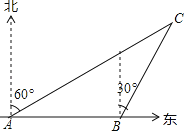
【题目】已知Rt△OAB，∠OAB＝90°，∠ABO＝30°，斜边OB＝4，将Rt△OAB绕点O顺时针旋转60°，连接BC

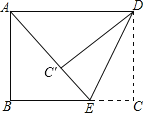
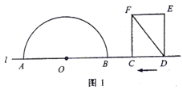
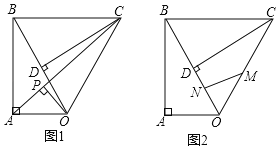
（1）如图1，连接AC，作OP⊥AC，垂足为P，求△AOC的面积和线段OP的长；

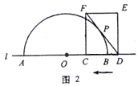
（2）如图2，点M是线段OC的中点，点N是线段OB上的动点（不与点O重合），求△CMN周长的最小值．

Answer 1

【答案】（1）S△AOC＝，OP＝；（2）2+2．

【解析】

（1）先根据勾股定理求出各边长AO、AB和角的度数，再根据旋转60°，可以知道Rt△ODC是旋转后得到的图形，其对应边和对应角都相等．从而求出BD、OC，并求出∠ABC＝90°，可求出△AOC的面积，利用三角形的面积公式计算OP即可；

（2）如图2，连接BM，AM，AC，根据等边三角形的性质得到BM⊥OC，根据全等三角形的性质得到BM＝AB，AO＝OM，得到AM被BD垂直平分，即M关于直线BO的对称点为A，连接AC，则C△CMN＝AC+MC，于是得到结论．

解：（1）∵∠OAB＝90°，∠ABO＝30°，斜边OB＝4，

∴∠AOB＝60°，AO＝2，AB＝，

∵Rt△OAB绕点O顺时针旋转60°，得到Rt△ODC，

∴OC＝4，OD＝2，∠ODC＝90°，∠DOC＝60°，CD＝，

∴BD＝4﹣OD＝4﹣2＝2，

∴在Rt△BDC中，BC＝＝OC，

∴∠OBC＝∠COB＝60°，

∴∠ABC＝60°+30°＝90°，△OBC为等边三角形，

∴S△AOC＝，

∴AC＝＝2，

∴OP＝；

（2）如图2，连接BM，AM，

∵M为OC中点，△OBC为等边三角形，

∴BM⊥OC，

在Rt△AOB中，∠A＝90°，∠ABO＝30°，

∴∠BOA＝60°，

∵∠BOC＝60°，

∴∠BOA＝∠BOM，

∵∠BAO＝∠BMO＝90°，BO＝BO，

∴△BAO≌△BMO（ASA），

∴BM＝AB，AO＝OM，

∴B，O在AM的中垂线上，

∴AM被BD垂直平分，

即M关于直线BO的对称点为A，

连接AC，当N为AC与BO的交点时，MN+NC最短为AC,此时C△CMN＝AC+MC，

∵M是OC的中点，

∴MC＝OC＝2，

∴C△CMN的最小值为2+2．