Question

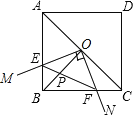
【题目】如图，在ABCD中，按下列步骤作图：

①以点B为圆心，以适当长为半径作弧，交AB于点M．交BC于点N；

②再分别以点M和点N为圆心，大于MN的长为半径作弧，两弧交于点G；

③作射线BG交AD于F；

④过点A作AE⊥BF交BF于点P，交BC于点E；

⑤连接EF，PD．

（1）求证：四边形ABEF是菱形；

（2）若AB＝4，AD＝6，∠ABC＝60°，求DP的长．

Answer 1

【答案】（1）见解析；（2）2

【解析】

（1）根据线段垂直平分线的性质和平行四边形的性质即可得到结论；

（2）作PH⊥AD于H，根据四边形ABEF是菱形，∠ABC＝60°，AB＝4，得到AB＝AF＝4，∠ABF＝∠ADB＝30°，AP⊥BF，从而得到PH，DH＝5，然后利用勾股定理求解即可．

解：（1）证明：由作图知BA＝BE，∠ABF＝∠EBF，

∵四边形ABCD是平行四边形，

∴AD∥BC，

∴∠EBF＝∠AFB，

∴∠ABF＝∠AFB，

∴AB＝AF＝BE，

∴四边形ABEF是平行四边形，

又AB＝BE，

∴四边形ABEF是菱形；

（2）解：作PH⊥AD于H，

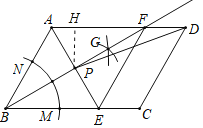
∵四边形ABEF是菱形，∠ABC＝60°，AB＝4，

∴AB＝AF＝4，∠ABF＝∠AFB＝30°，AP⊥BF，

∴APAB＝2，

∴PH，DH＝5，

∴DP2．