题目内容
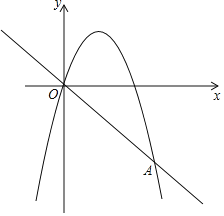
【题目】如图,平面直角坐标系xOy中,点A,B,C,D都在边长为1的小正方形网格的格点上,过点M(1,-2)的抛物线y=mx2+2mx+n(m>0)可能还经过( )
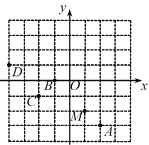
A.点AB.点BC.点CD.点D
【答案】D
【解析】
根据题意和过点M(1,-2)的抛物线![]() ,可以求得m和n的关系,从而可以判断各个选项中的点是否可能在该抛物线上,本题得以解
,可以求得m和n的关系,从而可以判断各个选项中的点是否可能在该抛物线上,本题得以解
决.
解: ∵抛物线![]() 过点M(1,-2)
过点M(1,-2)
∴m+2m+n=-2
即3m+n=-2.
若抛物线![]() 过点A (2,-3),则4m+4m+n=5m+ (3m+n) =-3.得m=-0.2与m>0矛盾. 故选项A不符合题意,
过点A (2,-3),则4m+4m+n=5m+ (3m+n) =-3.得m=-0.2与m>0矛盾. 故选项A不符合题意,
若抛物线![]() 过点B (-1, 0),则m-2m+n=-4m+ (3m+n) =0.得m=-0.5与m>0矛盾,故选项B不符合题意,
过点B (-1, 0),则m-2m+n=-4m+ (3m+n) =0.得m=-0.5与m>0矛盾,故选项B不符合题意,
若抛物线![]() 过点C(-2,-1),则4m-4m+n=-3m+ (3m+n) =-1.得
过点C(-2,-1),则4m-4m+n=-3m+ (3m+n) =-1.得![]() 与m>0矛盾,故选项C不符合题意.
与m>0矛盾,故选项C不符合题意.
若抛物线![]() 过点D(-4, 1),则16m-8m+n=5m+ (3m+n) =1.得
过点D(-4, 1),则16m-8m+n=5m+ (3m+n) =1.得![]() .故选项D符合题意.
.故选项D符合题意.
故选: D.

练习册系列答案
相关题目