题目内容
【题目】综合题
(1)抛物线m1:y1=a1x2+b1x+c1中,函数y1与自变量x之间的部分对应值如表:
设抛物线m1的顶点为P,与y轴的交点为C,则点P的坐标为 , 点C的坐标为 .
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2 , 则当x=-3时,y2= .
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3 . 设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由.
【答案】
(1)P(1,4),C(0,3)
(2)12
(3)解:存在.
当y1=0时,-x2+2x+3=0,解得x1=-1,x2=3,则A(-1,0),B(3,0),
∵抛物线m1沿水平方向平移,得到抛物线m3,
∴CK∥AM,CK=AM,
∴四边形AMKC为平行四边形,
当CA=CK时,四边形AMKC为菱形,而AC= ![]() ,则CK=
,则CK= ![]() ,
,
当抛物线m1沿水平方向向右平移 ![]() 个单位,此时K(
个单位,此时K( ![]() ,3);当抛物线m1沿水平方向向左平移
,3);当抛物线m1沿水平方向向左平移 ![]() 个单位,此时K(-
个单位,此时K(- ![]() ,3)
,3)
【解析】解:(1)把(-1,0),(1,4),(2,3)分别代入y1=a1x2+b1x+c1得
 ,解得
,解得 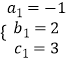 .
.
所以抛物线m1的解析式为y1=-x2+2x+3=-(x-1)2+4,则P(1,4),
当x=0时,y=3,则C(0,3);
( 2 )因为抛物线m1沿x轴翻折,得到抛物线m2,
所以y2=(x-1)2-4,当x=-3时,y2=(x+1)2-4=(-3-1)2-4=12.
【考点精析】根据题目的已知条件,利用坐标与图形变化-平移的相关知识可以得到问题的答案,需要掌握新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案【题目】小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员 | 小丽 | 小华 |
月销售件数(件) | 200 | 150 |
月总收入(元) | 1400 | 1250 |
假设营业员的月基本工资为x元,销售每件服装奖励y元.
(1)求x、y的值;
(2)若营业员小丽某月的总收入不低于1800元,那么小丽当月至少要卖服装多少件?
(3)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需315元;如果购买甲1件,乙2件,丙3件共需285元.某顾客想购买甲、乙、丙各一件共需 元.
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.





