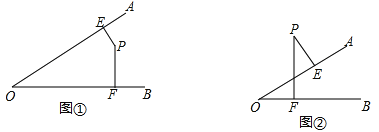题目内容
【题目】如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.

解:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(
即∠ =∠ ( )
∴∠3=∠
∴AD∥BE( )
【答案】BAF;两直线平行,同位角相等;BAF;等量代换;等式的性质;角的和差;CAD;内错角相等,两直线平行.
【解析】∵AB∥CD(已知),
∴∠4=∠BAE(两直线平行,同位角相等);
∵∠3=∠4(已知),
∴∠3=∠BAE(等量代换);
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF(等式的性质),
即∠BAE=∠DAC,
∴∠3=∠DAC(等量代换),
∴AD∥BE(内错角相等,两直线平行)。

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
【题目】在一次中学生田径运动会上,参加调高的15名运动员的成绩如下表所示:
成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 1 | 2 | 4 | 3 | 3 | 2 |
那么这些运动员跳高成绩的众数是( )
A.4 B.1.75 C.1.70 D.1.65