题目内容
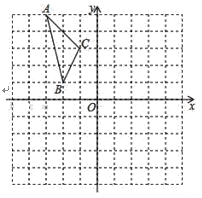
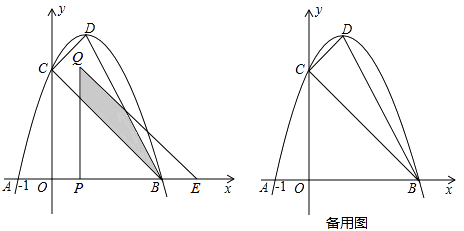
【题目】如图,抛物线 ![]() 与
与 ![]() 轴交于点
轴交于点 ![]() (点
(点 ![]() 分别在
分别在 ![]() 轴的左右两侧)两点,与
轴的左右两侧)两点,与 ![]() 轴的正半轴交于点
轴的正半轴交于点 ![]() ,顶点为
,顶点为 ![]() ,已知点
,已知点 ![]() .
.
(1)求点 ![]() 的坐标;
的坐标;
(2)判断△ ![]() 的形状,并说明理由;
的形状,并说明理由;
(3)将△ ![]() 沿
沿 ![]() 轴向右平移
轴向右平移 ![]() 个单位(
个单位( ![]() )得到△
)得到△ ![]() .△
.△ ![]() 与△
与△ ![]() 重叠部分(如图中阴影)面积为
重叠部分(如图中阴影)面积为 ![]() ,求
,求 ![]() 与
与 ![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量 ![]() 的取值范围.
的取值范围.
【答案】
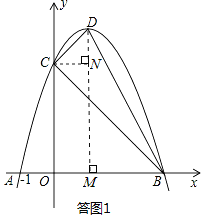
(1)解:如答题1所示:
∵点A(-1,0)在抛物线y=-(x-1)2+c上,
∴0=-(-1-1)2+c,得c=4,
∴抛物线解析式为:y=-(x-1)2+4,
令x=0,得y=3,∴C(0,3);
令y=0,得x=-1或x=3,∴B(3,0).
(2)解:△CDB为直角三角形.理由如下:
由抛物线解析式,得顶点D的坐标为(1,4).
如答图1所示,过点D作DM⊥x轴于点M,则OM=1,DM=4,BM=OB-OM=2.
过点C作CN⊥DM于点N,则CN=1,DN=DM-MN=DM-OC=1.
在Rt△OBC中,由勾股定理得:BC= ![]() ;
;
在Rt△CND中,由勾股定理得:CD= ![]() ;
;
在Rt△BMD中,由勾股定理得:BD= ![]() .
.
∵BC2+CD2=BD2,
∴△CDB为直角三角形(勾股定理的逆定理)
(3)解:设直线BC的解析式为y=kx+b,∵B(3,0),C(0,3),
∴ ![]() ,
,
解得k=-1,b=3,
∴y=-x+3,
直线QE是直线BC向右平移t个单位得到,
∴直线QE的解析式为:y=-(x-t)+3=-x+3+t;
设直线BD的解析式为y=mx+n,∵B(3,0),D(1,4),
∴ ![]() ,
,
解得:m=-2,n=6,
∴y=-2x+6.
连接CQ并延长,射线CQ交BD于点G,则G( ![]() ,3).
,3).
在△COB向右平移的过程中:
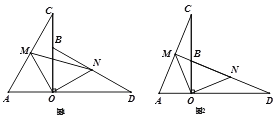
(I)当0<t≤ ![]() 时,如答图2所示:
时,如答图2所示:

设PQ与BC交于点K,可得QK=CQ=t,PB=PK=3-t.
设QE与BD的交点为F,则:
![]() ,解得
,解得 ![]() ,
,
∴F(3-t,2t).
S=S△QPE-S△PBK-S△FBE= ![]() PEPQ-
PEPQ- ![]() PBPK-
PBPK- ![]() BEyF=
BEyF= ![]() ×3×3-
×3×3- ![]() (3-t)2-
(3-t)2- ![]() t2t=-
t2t=- ![]() t2+3t;
t2+3t;
(II)当 ![]() <t<3时,如答图3所示:
<t<3时,如答图3所示:
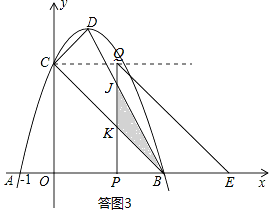
设PQ分别与BC、BD交于点K、点J.
∵CQ=t,
∴KQ=t,PK=PB=3-t.
直线BD解析式为y=-2x+6,令x=t,得y=6-2t,
∴J(t,6-2t).
S=S△PBJ-S△PBK= ![]() PBPJ-
PBPJ- ![]() PBPK=
PBPK= ![]() (3-t)(6-2t)-
(3-t)(6-2t)- ![]() (3-t)2=
(3-t)2= ![]() t2-3t+
t2-3t+ ![]() .
.
综上所述,S与t的函数关系式为:
S= 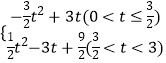 .
.
【解析】(1)首先用待定系数法,将点A的坐标代入函数解析式,求出c的值,就可以求出抛物线的解析式,然后由x=0,求出函数值,得到点C的坐标,由y=0,建立方程求出自变量的值,得到点B的坐标。
(2)利用勾股定理分别求出△CDB三边的平方,利用勾股定理的逆定理,求较小两边的平方和是否等于最大边的平方,判定△CDB为直角三角形。
(3)先分别求出直线BC的解析式、直线QE的解析式、直线BD的解析式及点G的坐标。△COB沿x轴向右平移过程中,分两个阶段:当0<t≤![]() 时,如图2所示,此时重叠部分为一个四边形,根据S=S△QPE-S△PBK-S△FBE,即可求出结果;当
时,如图2所示,此时重叠部分为一个四边形,根据S=S△QPE-S△PBK-S△FBE,即可求出结果;当 ![]() <t<3时,如答图3所示,根据S=S△PBJ-S△PBK,即可求出结果。
<t<3时,如答图3所示,根据S=S△PBJ-S△PBK,即可求出结果。
【考点精析】本题主要考查了确定一次函数的表达式和勾股定理的逆定理的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案