题目内容
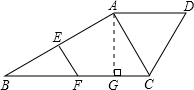
如图,在梯形ABCD中,AD∥BC,AC⊥AB,∠B=30°,AD=DC,E是AB中点,EF∥AC交BC于点F,且EF=
,求梯形ABCD的面积.

| 3 |

过点A作AG⊥BC于点G.
∵E是AB中点,且EF∥AC,
∴EF是△ABC的中位线.
∵EF=
,
∴AC=2EF=2
.
∵∠B=30°且AC⊥AB,
∴∠ACB=60°,BC=4
.
∵AD∥BC,
∴∠CAD=60°.
又AD=DC,
∴△ACD是等边三角形.
∴AD=2
.
在Rt△ACG中,∠AGC=90°,∠ACG=60°,AC=2
,
∴AG=3.
∴S梯形ABCD=
(2
+4
)•3=9
.
∵E是AB中点,且EF∥AC,
∴EF是△ABC的中位线.
∵EF=
| 3 |
∴AC=2EF=2
| 3 |
∵∠B=30°且AC⊥AB,
∴∠ACB=60°,BC=4
| 3 |
∵AD∥BC,
∴∠CAD=60°.
又AD=DC,
∴△ACD是等边三角形.
∴AD=2
| 3 |
在Rt△ACG中,∠AGC=90°,∠ACG=60°,AC=2
| 3 |
∴AG=3.
∴S梯形ABCD=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |


练习册系列答案
相关题目




