题目内容
如图,梯形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点.已知两底差是6,两腰和是16,则△EFG的周长是______.


连接AE,并延长交CD于K,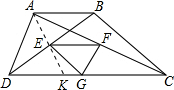
∵AB∥CD,
∴∠BAE=∠DKE,∠ABD=∠EDK,
∵点E、F、G分别是BD、AC、DC的中点.
∴BE=DE,
∴△AEB≌△KED,
∴DK=AB,AE=EK,EF为△ACK的中位线,
∴EF=
CK=
(DC-DK)=
(DC-AB),
∵EG为△BCD的中位线,
∴EG=
BC,
又FG为△ACD的中位线,
∴FG=
AD,
∴EG+GF=
(AD+BC),
∵两腰和是16,即AD+BC=16,两底差是6,即DC-AB=6,
∴EG+GF=8,FE=3,
∴△EFG的周长是8+3=11.
故答案为:11.

∵AB∥CD,
∴∠BAE=∠DKE,∠ABD=∠EDK,
∵点E、F、G分别是BD、AC、DC的中点.
∴BE=DE,
∴△AEB≌△KED,
∴DK=AB,AE=EK,EF为△ACK的中位线,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵EG为△BCD的中位线,
∴EG=
| 1 |
| 2 |
又FG为△ACD的中位线,
∴FG=
| 1 |
| 2 |
∴EG+GF=
| 1 |
| 2 |
∵两腰和是16,即AD+BC=16,两底差是6,即DC-AB=6,
∴EG+GF=8,FE=3,
∴△EFG的周长是8+3=11.
故答案为:11.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



