题目内容
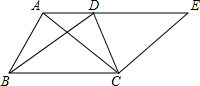
在等腰△ABC中，AB=AC，BD⊥AC，CE⊥AB，垂足分别为点D，E，连接ED，试说明四边形EBCD是等腰梯形．
证明：∵△ABC是等腰三角形，
∴AB=AC，
∴∠ABC=∠ACB，
∵BD⊥AC，CE⊥AB，
∴∠BEC=∠CDB=90°，
在△EBC和△DCB中，
，
∴△EBC≌△DCB（AAS），
∴EB=DC，
∴AB-EB=AC-DC，
即AE=AD，
∴∠AED=∠ADE，
∵∠A+∠AED+∠ADE=180°，∠A+∠ABC+∠ACB=180°，
∴∠AED=∠ABC，
∴ED∥CB，
∴四边形EBCD是等腰梯形．
∴AB=AC，
∴∠ABC=∠ACB，
∵BD⊥AC，CE⊥AB，
∴∠BEC=∠CDB=90°，
在△EBC和△DCB中，
|
∴△EBC≌△DCB（AAS），
∴EB=DC，
∴AB-EB=AC-DC，
即AE=AD，
∴∠AED=∠ADE，
∵∠A+∠AED+∠ADE=180°，∠A+∠ABC+∠ACB=180°，
∴∠AED=∠ABC，
∴ED∥CB，
∴四边形EBCD是等腰梯形．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
相关题目
