题目内容
如图，在梯形ABCD中，AD∥BC，AB⊥BC，E是CD的中点，且AB=AD+BC，判断△ABE的形状，并说明理由．
△ABE是等腰直角三角形．
理由是：延长AE交BC的延长线于M，
∵AD∥BM，
∴∠DAE=∠M，
∵∠AED=∠CEM，DE=EC，
∴△ADE≌△MEC，
∴AD=CM，
∵AB=AD+BC，
∴AB=BM，
∴△ABM是等腰直角三角形，
∵△ADE≌△MCE，
∴AE=EM，
∵∠ABC=90°，
∴BE⊥AM，BE=
AM=AE，
∴△AEB是等腰直角三角形．
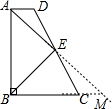
理由是：延长AE交BC的延长线于M，
∵AD∥BM，
∴∠DAE=∠M，
∵∠AED=∠CEM，DE=EC，
∴△ADE≌△MEC，
∴AD=CM，
∵AB=AD+BC，
∴AB=BM，
∴△ABM是等腰直角三角形，
∵△ADE≌△MCE，
∴AE=EM，
∵∠ABC=90°，
∴BE⊥AM，BE=
| 1 |
| 2 |
∴△AEB是等腰直角三角形．
练习册系列答案
出彩同步大试卷系列答案
相关题目
