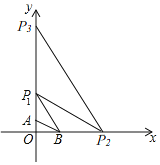Question

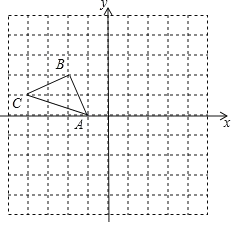
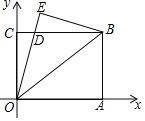
【题目】如图，四边形为长方形，点在轴上，点在轴上，点坐标为，将沿翻折，的对应点为交于点，则点的坐标为__________．

Answer 1

【答案】（，6）

【解析】

由四边形OABC为矩形，A在x轴上，C在y轴上，B点坐标为（8，6），可求得矩形的边长，然后由将△OAB沿OB翻折，A的对应点为E，可求得△OBD是等腰三角形，然后设CD=x，由勾股定理即可求得答案．

∵四边形OABC为矩形，A在x轴上，C在y轴上，B点坐标为（8，6），

∴OC=AB=6，BC=OA=8，∠OCB=90°，BC∥OA，

∴∠AOB=∠OBC，

∵将△OAB沿OB翻折，A的对应点为E，

∴∠EOB=∠AOB，

∴∠OBC=∠EOB，

∴OD=BD，

设CD=x，则OD=BC-CD=8-x，

在Rt△OCD中，OC2+CD2=OD2，

∴x2+62=（8-x）2，

解得：x=，

∴点D的坐标为（，6）．

故答案为：（，6）．