题目内容
【题目】![]() 是等边三角形,
是等边三角形,![]() 为平面内的一个动点,
为平面内的一个动点,![]() ,
,![]() 平分
平分![]() ,且
,且![]() .
.
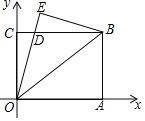
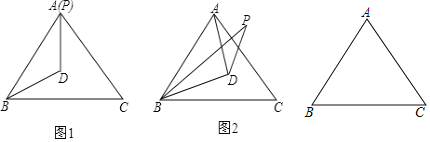
(1)当![]() 与
与![]() 重合时(如图1),求
重合时(如图1),求![]() 的度数;
的度数;
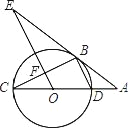
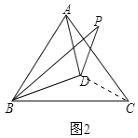
(2)当![]() 在
在![]() 的内部时(如图2),求
的内部时(如图2),求![]() 的度数;
的度数;
(3)当![]() 在
在![]() 的外部时,请你直接写出
的外部时,请你直接写出![]() 的度数为 .
的度数为 .
【答案】(1)![]() ;(2)
;(2)![]() ;(3)30°或150°
;(3)30°或150°
【解析】
(1)由于P,A重合,DP=DB,∠DBP=∠BPD,因为DB是∠PBC的平分线,可得∠DBP=∠BPD=30°;
(2)连接CD,由“SAS”可证△PBD≌△CBD,可得∠BPD=∠BCD,由“SSS”可证△BCD≌△ACD,可得∠BCD=∠ACD=![]() ∠ACB=30°,即可求解;
∠ACB=30°,即可求解;
(3)分三种情况:①当BP在AB的左侧,BD在△ABC内部时;②当BP,BD都在三角形外部,且∠BPD为锐角时;③当BP,BD都在△ABC外部,且∠BPD为钝角时,同(2)中的步骤分别求解.连接CD,步骤有2个,一是证明△PBD≌△CBD,从而得出∠BPD=∠BCD,二是证明△BCD≌△ACD,得出∠BCD=∠ACD,从而可得出结果.
解:(1)∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ;
;
(2)连接![]() ,
,
∵点![]() 在
在![]() 的平分线上,
的平分线上,
∴![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴![]() .
.
在![]() 和
和![]() 中,
中,
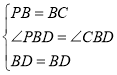 ,
,
∴![]() .
.
∴![]() .
.
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)如图3,连接CD,
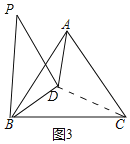
同(2)可得△ACD≌△BCD(SSS),
∴∠ACD=∠BCD=30°,
同(2)可得△PBD≌△CBD(SAS),
∴∠BPD=∠BCD=30°;
如图4,连接CD,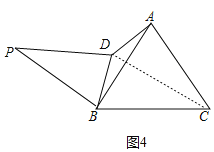
同理可得△ACD≌△BCD(SSS),
∴∠ACD=∠BCD=30°,
同理可得△PBD≌△CBD(SAS),
∴∠BPD=∠BCD=30°;
如图5,连接CD,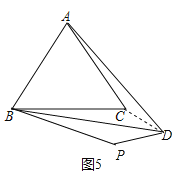
同理可得△ACD≌△BCD(SSS),
∴∠ACD=∠BCD=(360°-60°)÷2=150°,
同理可得△PBD≌△CBD(SAS)
∴∠BPD=∠BCD=150°.
综上可知,∠BPD的度数为30°或150°,
故答案为:30°或150°.