题目内容
【题目】如图,平面直角坐标系中有点A(0,1)、B(![]() ,0).
,0).
连接AB,以A为圆心,以AB为半径画弧,交y轴于点P1;
连接BP1,以B为圆心,以BP1为半径画弧,交x轴于点P2;
连接P1P2,以P1为圆心,以P1P2为半径画弧,交y轴于点P3;
按照这样的方式不断在坐标轴上确定点Pn的位置,那么点P6的坐标是_____.
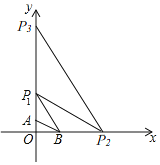
【答案】(27![]() ,0)
,0)
【解析】
利用勾股定理和坐标轴上点的坐标特征分别求出P1、P2、P3的坐标,然后利用坐标变换规律写出P4,P5,P6的坐标.
解:由题意知OA=1,OB=![]() ,
,
则AB=AP1=![]() =2,
=2,
∴点P1(0,3),
∵BP1=BP2=![]() =2
=2![]() ,
,
∴点P2(3![]() ,0),
,0),
∵P1P3=P1P2=![]() =6,
=6,
∴点P3(0,9),
同理可得P4(9![]() ,0),P5(0,27),
,0),P5(0,27),
∴点P6的坐标是(27![]() ,0).
,0).
故答案为(27![]() ,0).
,0).

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目