题目内容
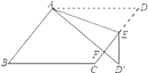
【题目】如图，在ABCD中，E为边CD上一点，将
沿AE折叠至
处，
与CE交于点
若
，
，则
的大小为________．
【答案】
【解析】
由平行四边形的性质得出∠D=∠B=52°，由折叠的性质得：∠D′=∠D=52°，∠EAD′=∠DAE=20°，由三角形的外角性质求出∠AEF=72°，与三角形内角和定理求出∠AED′=108°，即可得出∠FED′的大小．
解：∵四边形ABCD是平行四边形，
∴∠D=∠B=52°，
由折叠的性质得：∠D′=∠D=52°，∠EAD′=∠DAE=20°，
∴∠AEF=∠D+∠DAE=52°+20°=72°，∠AED′=180°-∠EAD′-∠D′=108°，
∴∠FED′=108°-72°=36°；
故答案为：36°．
练习册系列答案
相关题目
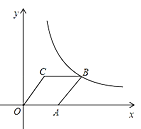
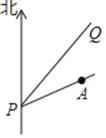
【题目】设边长为
的正方形的中心
在直线
上，它的一组对边垂直于直线，半径为
的圆的圆心
在直线上运动，、两点之间的距离为
．
（
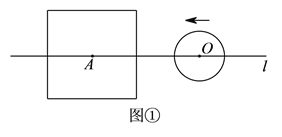
）如图①，当
时，填表：
| ⊙ |
|
|
|
|
| __________ |
| __________ |
| __________ |
（
）如图②，⊙与正方形有
个公共点
、
、
、
、
，求此时与
之间的数量关系：
（
）由（）可知，、、之间的数量关系和⊙与正方形的公共点个数密切相关．当
时，请根据、、
之间的数量关系，判断⊙与正方形的公共点个数．
（
）当与之间满足（）中的数量关系时，⊙与正方形的公共点个数为__________．