题目内容
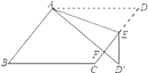
【题目】如图,点D、E分别是等边三角形ABC的边BC、AC上的点,连接AD、BE交于点O,且△ABD≌△BCE.
(1)若AB=3,AE=2,则BD= ;
(2)若∠CBE=15°,则∠AOE= ;
(3)若∠BAD=a,猜想∠AOE的度数,并说明理由.

【答案】(1)BD=1;(2)60°;(3)∠AOE =60°.
【解析】
(1)根据等边三角形的性质求出AC,得到EC,根据全等三角形的性质解答;
(2)根据全等三角形的性质得到∠BAD=∠CBE=15°,根据三角形的外角性质计算即可;
(3)仿照(2)的作法解答.
解:(1)∵△ABC是等边三角形,
∴AC=AB=3,
∴EC=AC-AE=1,
∵△ABD≌△BCE,
∴BD=EC=1,
故答案为:1;
(2)∵△ABD≌△BCE,
∴∠BAD=∠CBE=15°,
∵∠CBE=15°,
∴∠ABO=45°,
∴∠AOE=∠BAD+∠ABO=60°,
故答案为:60°;
(3)由(2)得,∠BAD=∠CBE,
∵∠ABO+∠CBE=60°,
∴∠AOE=∠BAD+∠ABO=60°.

练习册系列答案
相关题目