Question

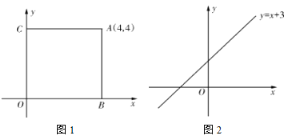
【题目】在平面直角坐标系xOy中，抛物线y＝﹣2x2+(m+9)x﹣6的对称轴是x＝2．

（1）求抛物线表达式和顶点坐标；

（2）将该抛物线向右平移1个单位，平移后的抛物线与原抛物线相交于点A，求点A的坐标；

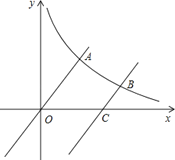
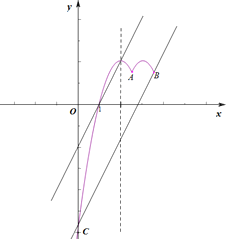
（3）抛物线y＝﹣2x2+(m+9)x﹣6与y轴交于点C，点A关于平移后抛物线的对称轴的对称点为点B，两条抛物线在点A、C和点A、B之间的部分（包含点A、B、C）记为图象M．将直线y＝2x﹣2向下平移b（b＞0）个单位，在平移过程中直线与图象M始终有两个公共点，请你写出b的取值范围　 　．

Answer 1

【答案】（1）y=﹣2x2+8x﹣6，顶点坐标为（2，2）；（2）A ()；（3）．

【解析】

（1）根据抛物线的对称轴公式求出m的值，进而求出抛物线的解析式以及顶点坐标；

（2）先求出平移后的抛物线解析式，然后求出交点坐标；

（3）根据图象即可写出b的取值范围．

（1）∵抛物线y=﹣2x2+（m+9）x﹣6的对称轴是x=2，

∴．

∴m=﹣1．

∴抛物线的表达式为y=﹣2x2+8x﹣6．

∴y=﹣2（x﹣2）2+2．

∴顶点坐标为（2，2）．

（2）由题意得，平移后抛物线表达式为y=﹣2（x﹣3）2+2，

∵﹣2（x﹣2）2=﹣2（x﹣3）2，

∴．

∴A ()．

（3）点A坐标为()，

则点B的坐标为，

设直线y=2x﹣2向下平移b（b＞0）个单位经过点B，

则y=2x﹣2﹣b，

故=7﹣2﹣b，

解得b=，

设直线y=2x﹣2向下平移b（b＞0）个单位经过点A，

=5﹣2﹣b，b=，

由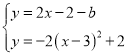，消去y得到：2x2﹣10x+14﹣b=0，

由题意：△=0，

∴100﹣8（14﹣b）=0，

∴b=，

观察图象可知：平移过程中直线与图象M始终有两个公共点，则．