题目内容
【题目】在平面直角坐标系中,过一点分别作![]() 轴,
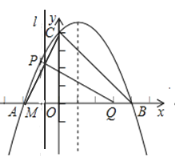
轴,![]() 轴的垂线,若其与两坐标轴围成的矩形的周长与面积相等,则这个点叫做和谐点.例如,图1中过点
轴的垂线,若其与两坐标轴围成的矩形的周长与面积相等,则这个点叫做和谐点.例如,图1中过点![]() 分别作
分别作![]() 轴,
轴,![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
,![]() ,矩形
,矩形![]() 的周长为
的周长为![]() ,面积也为
,面积也为![]() ,则点
,则点![]() 是和谐点.
是和谐点.
请根据以上材料回答下列问题:
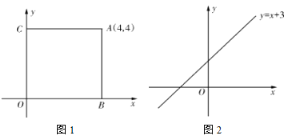
(1)若点![]() 是和谐点,则
是和谐点,则![]() ______;
______;
(2)若第一象限内的点![]() 与点
与点![]() 均为和谐点,求
均为和谐点,求![]() 的值;
的值;
(3)如图2,若点![]() 为和谐点,且在直线
为和谐点,且在直线![]() 上,求所有满足条件的
上,求所有满足条件的![]() 点的坐标.
点的坐标.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ;(3)满足条件的
;(3)满足条件的![]() 点分别是
点分别是![]() 或
或![]() .
.
【解析】
(1)根据题意列出关于a的方程,再解方程即可解答;
(2)利用和谐点定义列出方程组,求出方程组的解,然后再代入即可解答;
(3)设P(c,c+3),利用和谐点定义列出方程,分类讨论x的范围并求x的值,即可确定出P坐标.
(1)根据题意得:2(|a|+5)=5|a|,
解得:a=![]() 或
或![]() ;
;
故答案为![]() 或
或![]() ;
;
(2)![]() 第一象限内的点
第一象限内的点![]() 与点
与点![]() 均为和谐点,
均为和谐点,
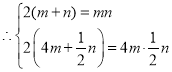
化简并整理得![]() .
.
![]()
(3)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,设
,设![]() 点坐标为
点坐标为![]() .
.
根据题意有![]() ,
,
①当![]() 时,方程为
时,方程为![]() .
.
整理得![]() .
.
解得![]() ,
,![]() (舍去).
(舍去).
![]() .
.
②当![]() 时,方程为
时,方程为![]() .
.
整理得![]() .
.
此方程无解.
③当![]() 时,方程为
时,方程为![]() .
.
整理得![]() .
.
解得![]() ,
,![]() (舍去).
(舍去).
![]() .
.
综上所述,满足条件的![]() 点分别是
点分别是![]() 或
或![]() .
.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目