题目内容
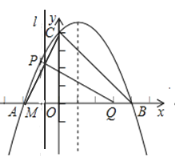
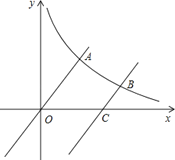
【题目】如图,已知函数![]() 与反比例函数
与反比例函数![]() (x>0)的图象交于点A.将
(x>0)的图象交于点A.将![]() 的图象向下平移6个单位后与双曲线
的图象向下平移6个单位后与双曲线![]() 交于点B,与x轴交于点C.
交于点B,与x轴交于点C.
(1)求点C的坐标;
(2)若![]() ,求反比例函数的解析式.
,求反比例函数的解析式.
【答案】(1)C点坐标为(![]() ,0);(2)
,0);(2)![]() .
.
【解析】
(1)根据一次函数图象的平移问题由![]() 的图象向下平移6个单位得到直线BC的解析式为
的图象向下平移6个单位得到直线BC的解析式为![]() ,然后把y=0代入即可确定C点坐标.
,然后把y=0代入即可确定C点坐标.
(2)作AE⊥x轴于E点,BF⊥x轴于F点,易证得Rt△OAE∽△RtCBF,则![]() ,若设A点坐标为(a,
,若设A点坐标为(a,![]() ),则CF=
),则CF=![]() ,BF=
,BF=![]() ,得到B点坐标为(
,得到B点坐标为(![]() ,
,![]() ),然后根据反比例函数上点的坐标特征得
),然后根据反比例函数上点的坐标特征得![]() ,解得a=3,于是可确定点A的坐标为(3,4),再利用待定系数法确定反比例函数的解析式.
,解得a=3,于是可确定点A的坐标为(3,4),再利用待定系数法确定反比例函数的解析式.
解:(1)∵![]() 的图象向下平移6个单位后与双曲线
的图象向下平移6个单位后与双曲线![]() 交于点B,与x轴交于点C,
交于点B,与x轴交于点C,

∴直线BC的解析式为![]() .
.
把y=0代入得![]() ,解得x=
,解得x=![]() .
.
∴C点坐标为(![]() ,0).
,0).
(2)作AE⊥x轴于E点,BF⊥x轴于F点,如图,
∵OA∥BC,∴∠AOB=∠BCF.
∴Rt△OAE∽△RtCBF.∴![]() .
.
设A点坐标为(a,![]() ),则OE=a,AE=
),则OE=a,AE=![]() ,
,
∴CF=![]() ,BF=
,BF=![]() .∴OF=OC+CF=
.∴OF=OC+CF=![]() .
.
∴B点坐标为(![]() ,
,![]() ).
).
∵点A与点B在![]() 的图象上,
的图象上,
∴![]() ,解得a=3.∴点A的坐标为(3,4).
,解得a=3.∴点A的坐标为(3,4).
把A(3,4)代入![]() 得k=3×4=12.
得k=3×4=12.
∴反比例函数的解析式为![]() .
.

练习册系列答案
相关题目