Question

【题目】如图，正的边长为2，过点的直线，且与关于直线对称.

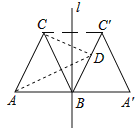
（Ⅰ）连接，判断四边形的形状并进行证明.

（Ⅱ）为线段上一动点，求的最小值.

Answer 1

【答案】（Ⅰ）结论：四边形是菱形.证明见解析；（Ⅱ）的最小值为4.

【解析】

（1）连接，根据菱形的判定定理解答.

(2) 连接CC′，根据△ABC、△A′BC′均为正三角形即可得出四边形A′BCC′为菱形，进而得出点C关于BC'对称的点是A'，以此确定当点D与点B重合时，AD+CD的值最小，代入数据即可得出结论．

（Ⅰ）结论：四边形是菱形.

证明：∵和均为正三角形，

∴，

∵，且与关于直线对称，

∴，，

∴是正三角形，.

∴，

∴四边形是菱形.

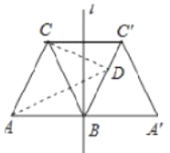
（Ⅱ）∵四边形是菱形，

∴点关于直线的对称点为，

∴当点与点重合时，取得最小值，

此时，，

即：的最小值为4.