题目内容
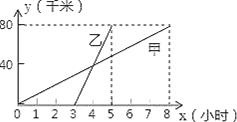
【题目】甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地，行驶过程中的函数图象如图所示，请根据图象回答下列问题：
(1)甲先出发______小时后，乙才出发；大约在甲出发______小时后，两人相遇，这时他们离A地_______千米.
(2)两人的行驶速度分别是多少？
(3)分别写出表示甲、乙的路程y(千米)与时间x(小时)之间的函数表达式(不要求写出自变量的取值范围).
【答案】（1）3；4；40．（2）甲的速度10km/h；乙的速度40km/h．（3）甲的函数表达式：y＝10x；乙的函数表达式：y＝40x120．
【解析】
（1）结合图象，由速度＝路程÷时间，即可得出结论，求出甲、乙的速度，根据待定系数法，可求出乙的函数表达式，结合甲的速度依据甲的图象过原点，可得出甲的函数表达式；
（2）（3）由（1）所求即可写出结论.
（1）根据图像可得：
甲的速度：80÷8＝10km/h；
乙的速度：80÷（53）＝40km/h．
∵甲的速度为10km/h，且过原点（0，0），
∴甲的函数表达式：y＝10x；
设乙的函数表达式为y＝kx＋b，
∵点（3，0）和（5，80）在乙的图象上，
∴有
，解得：
．
故乙的函数表达式：y＝40x120．
由图可得甲先出发3小时后，乙才出发；
令y＝10x=40x120，解得x=4，此时y=40，
∴在甲出发4小时后，两人相遇，这时他们离A地40千米.
故答案为：3；4；40．
（2）由（1）得甲的速度10km/h；乙的速度40km/h．
（3）由（1）甲的函数表达式：y＝10x；乙的函数表达式：y＝40x120．
阅读快车系列答案
【题目】重庆市的重大惠民工程﹣﹣公租房建设已陆续竣工，计划10年内解决低收入人群的住房问题，前6年，每年竣工投入使用的公租房面积y（单位：百万平方米），与时间x的关系是y=
x+5，（x单位：年，1≤x≤6且x为整数）；后4年，每年竣工投入使用的公租房面积y（单位：百万平方米），与时间x的关系是y=-
x+
（x单位：年，7≤x≤10且x为整数）．假设每年的公租房全部出租完．另外，随着物价上涨等因素的影响，每年的租金也随之上调，预计，第x年投入使用的公租房的租金z（单位：元/m2）与时间x（单位：年，1≤x≤10且x为整数）满足一次函数关系如下表：
z（元/m2） | 50 | 52 | 54 | 56 | 58 | … |
x（年） | 1 | 2 | 3 | 4 | 5 | … |
（1）求出z与x的函数关系式；
（2）求政府在第几年投入的公租房收取的租金最多，最多为多少百万元；
（3）若第6年竣工投入使用的公租房可解决20万人的住房问题，政府计划在第10年投入的公租房总面积不变的情况下，要让人均住房面积比第6年人均住房面积提高a%，这样可解决住房的人数将比第6年减少1.35a%，求a的值．
（参考数据：
，
，
）
【题目】2017年12月，旗团委号召各校组织开展捐赠衣物的“暖冬行动”
某校七年级六个班参加了这次捐赠活动，若每班捐赠衣物以100件为基准，超过的件数用正数表示，不足的件数用负数表示，记录如下：
班级 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
人数 | 40 | 43 | 45 | 44 | 40 | 38 |
件数 |
|
|
|
|
|
|
捐赠衣物最多的班比最少的班多多少件？
该校七年级学生共捐赠多少件衣物？该校七年级学生平均每人捐赠多少件衣物？
