题目内容
【题目】如图，已知直线y=﹣x﹣（k+1）与双曲线y= 
相交于B、C两点，与x轴相交于A点，BM⊥x轴交x轴于点M，S△OMB= 
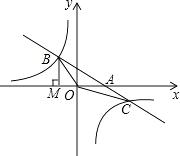
（1）求这两个函数的解析式；
（2）若已知点C的横坐标为3，求A、C两点坐标；
（3）在（2）条件下，是否存在点P，使以A、O、C、P为顶点的四边形是平行四边形？若存在，请直接写出P点的坐标；若不存在，请说明理由．
【答案】
（1）
解：∵S△OMB= 
= 
×OM×BM= |k|，由反比例函数图象在第二、四象限，
∴k=﹣3，
∴这两个函数的解析式分别为：y=﹣ 
，y=﹣x+2
（2）
解：在y=﹣x+2中，
设y=0，则x=2，
所以A（2，0），
将x=3代入y=﹣ 得，y=﹣1，
所以C（3，﹣1）
（3）
解：当AO是对角线时，由C点坐标（3，﹣1），可得：点P1（﹣1，1）；
当OC是对角线时，AO=P2C=2，则点P2（1，﹣1）；
当AC是对角线时，AO=CP3，则点P3（5，﹣1）；
故存在P（﹣1，1）或（1，﹣1）或（5，﹣1），使以A、O、C、P为顶点的四边形为平行四边形．
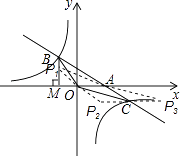
【解析】（1）利用S△OMB= ，结合反比例函数图象的性质得出k的值，进而得出答案；（2）利用图象上点的坐标性质分别求出A，C点坐标；（3）以两边为邻边，另一边为对角线画平行四边形是可行的，所以点P存在．
【考点精析】解答此题的关键在于理解一次函数的概念的相关知识，掌握一般地，如果y=kx+b（k，b是常数，k不等于0），那么y叫做x的一次函数，以及对反比例函数的概念的理解，了解形如y＝k/x（k为常数，k≠0）的函数称为反比例函数．自变量x的取值范围是x不等于0的一切实数，函数的取值范围也是一切非零实数．
名师点睛字词句段篇系列答案
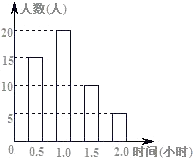
【题目】某水果公司购进10 000kg苹果，公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计，部分结果如下表：
苹果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
损坏苹果质量m(kg) | 10.50 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
苹果损坏的频率 (结果保留小数点后三位) | 0.105 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
估计这批苹果损坏的概率为_____(结果保留小数点后一位)，损坏的苹果约有______kg．
【题目】有这样一个问题：探究函数
的图象与性质．
小华根据学习函数的经验，对函数
的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)函数
的自变量x的取值范围是 ；
(2)下表是y与x的几组对应值.
x | … | -3 | -2 | -1 | 0 |
| 1 | 3 |
| 4 | 5 | 6 | 7 | … |
y | … |
|
|
|
|
| 6 | 6 |
|
|
|
| m | … |
求m的值；
（3）如下图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点.根据描出的点，画出该函数的图象；
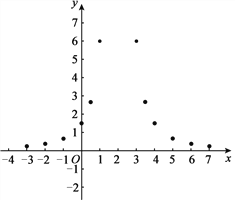
（4）结合函数的图象，写出该函数的一条性质： .
