题目内容
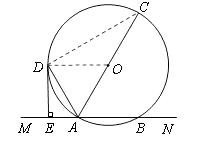
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
【答案】
(1)证明:连接OD,
∵OA=OD,∴∠OAD=∠ODA。
∵∠OAD=∠DAE,∴∠ODA=∠DAE。∴DO∥MN,
∵DE⊥MN,∴∠ODE=∠DEM =90°,即OD⊥DE。
∵D在⊙O上,∴DE是⊙O的切线
(2)解:连接CD,
 ,
,
∵∠AED=90°,DE=6,AE=3,∴AD= ![]() ,
,
∵AC是⊙O的直径,∴∠ADC=∠AED =90°。
∵∠CAD=∠DAE,∴△ACD∽△ADE。 ∴ ![]() ,即
,即 ![]() 。
。
解得:AC=15,
∴⊙O的半径是7.5cm。
【解析】 (1)要证DE是⊙O的切线,因此连接OD,先根据OA=OD得出∠OAD=∠ODA,由AD平分∠CAM得出∠OAD=∠DAE,再证出∠ODA=∠DAE得到DO∥MN,由DE⊥MN,证得OD⊥DE。即可得出结论。
(2)根据已知易证△ACD∽△ADE,根据相似三角形的对应边成比例,建立方程求解即可。
【考点精析】掌握平行线的性质和等腰三角形的性质是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;等腰三角形的两个底角相等(简称:等边对等角).

 名校课堂系列答案
名校课堂系列答案【题目】某同学进行社会调查,随机抽查了某个地区的20个家庭的收入情况,并绘制了统计图,请你根据统计图给出的信息回答:

(1)填写完成下表:
年收入(万元) | 0.6 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 9.7 |
户 数 | 1 | 1 | 2 | 4 |
这20个家庭的年平均收入为 万元;
(2)样本中的中位数是 万元,众数是 万元;
(3)在平均数、中位数两数中, 更能反映这个地区家庭的年收入水平.