题目内容
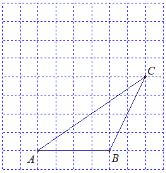
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是

A.4 B.3 C.2 D.1
【答案】B
【解析】
试题∵DE=BF,∴DF=BE。
∵在Rt△DCF和Rt△BAE中,CD=AB,DF=BE,∴Rt△DCF≌Rt△BAE(HL)。
∴FC=EA。故①正确。
∵AE⊥BD于点E,CF⊥BD于点F,∴AE∥FC。
∵FC=EA,∴四边形CFAE是平行四边形。
∴EO=FO。故②正确。
∵Rt△DCF≌Rt△BAE,∴∠CDF=∠ABE。∴CD∥AB。
∵CD=AB,∴四边形ABCD是平行四边形。故③正确。
由上可得:△CDF≌△BAE,△CDO≌△BAO,△CDE≌△BAF,△CFO≌△AEO,△CEO≌△AFO,△ADF≌△CBE等。故④图中共有6对全等三角形错误。
故正确的有3个。故选B。

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目