题目内容
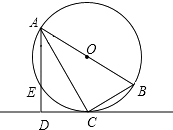
【题目】如图,将圆心角都是90°的扇形OAB和扇形OCD叠放在一起,连接AC、BD.
(1)将△AOC经过怎样的图形变换可以得到△BOD?
(2)若 ![]() 的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
【答案】
(1)解:∵扇形OAB和扇形OCD的圆心角都是90°,
∴OA=OB,OC=OD,∠AOB=∠COD=90°,
∴将△AOC绕点O顺时针旋转90°可以得到△BOD
(2)解:∵ ![]() =π,
=π,
∴OA=2,
∵△AOC绕点O顺时针旋转90°可以得到△BOD,
∴△AOC≌△BOD,
∴S△AOC=S△BOD,
∵S△AOC+S扇形COD=S△BOD+S扇形AOB+S阴影部分,
∴S阴影部分=S扇形COD﹣S扇形AOB= ![]() ﹣
﹣ ![]() =
= ![]() π(cm2)
π(cm2)
【解析】(1)扇形OAB和扇形OCD的圆心角都是90°,OA=OB,OC=OD,∠AOB=∠COD=90°,从而能判断出△AOC![]() △BOD ,根据旋转的性质知 将△AOC绕点O顺时针旋转90°可以得到△BOD;
△BOD ,根据旋转的性质知 将△AOC绕点O顺时针旋转90°可以得到△BOD;
(2)根据弧长计算公式及弧A B 的长度建立方程,从而求出OA的长,又由于△AOC≌△BOD,根据全等三角形的面积相等得出S△AOC=S△BOD,然后根据S△AOC+S扇形COD=S△BOD+S扇形AOB+S阴影部分,得S阴影部分=S扇形COD﹣S扇形AOB,算出答案。
【考点精析】解答此题的关键在于理解弧长计算公式的相关知识,掌握若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的,以及对扇形面积计算公式的理解,了解在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目