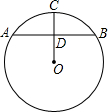
题目内容
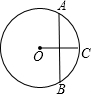
如图，⊙O的半径为2，弦AB=2
，点C在弦AB上，AC=
AB，则OC的长为（ ）
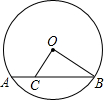
| 3 |
| 1 |
| 4 |
A．
| B．
| C．
| D．
|
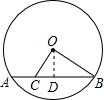
过点O作OD⊥AB于点D，
∵弦AB=2
，
∴AD=BD=
AB=
，AC=
AB=
，
∴CD=AD-AC=
，
∵⊙O的半径为2，
即OB=2，
∴在Rt△OBD中，OD=
=1，
在Rt△OCD中，OC=
=
．
故选D．
∵弦AB=2
| 3 |
∴AD=BD=
| 1 |
| 2 |
| 3 |
| 1 |
| 4 |
| ||
| 2 |
∴CD=AD-AC=
| ||
| 2 |
∵⊙O的半径为2，
即OB=2，
∴在Rt△OBD中，OD=
| OB2-BD2 |
在Rt△OCD中，OC=
| OD2+CD2 |
| ||
| 2 |
故选D．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
