Question

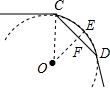
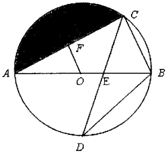
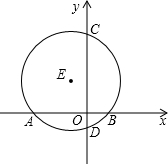
如图，AB是⊙O的直径，弦CD交AB于点E，OF⊥AC于点F，
（1）请探索OF和BC的关系并说明理由；
（2）若∠D=30°，BC=1时，求圆中阴影部分的面积．（结果保留π）

Answer 1

（1）OF∥BC，OF=

1

2

BC．
理由：由垂径定理得AF=CF．
∵AO=BO，
∴OF是△ABC的中位线．
∴OF∥BC，OF=

1

2

BC．

（2）连接OC．由（1）知OF=

1

2

．
∵AB是⊙O的直径，
∴∠ACB=90°．
∵∠D=30°，
∴∠A=30°．
∴AB=2BC=2．
∴AC=

3

．
∴S_△AOC=

1

2

×AC×OF=

3

4

．
∵∠AOC=120°，OA=1，
∴S_扇形AOC=

120•π•OA2

360

=

π

3

．
∴S_阴影=S_扇形AOC-S_△AOC=

π

3

-

3

4

．