题目内容
【题目】如图,基灯塔AB建在陡峭的山坡上,该山坡的坡度i=1:0.75.小明为了测得灯塔的高度,他首先测得BC=20m,然后在C处水平向前走了34m到达一建筑物底部E处,他在该建筑物顶端F处测得灯塔顶端A的仰角为43°.若该建筑物EF=20m,则灯塔AB的高度约为(精确到0.1m,参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93)( )
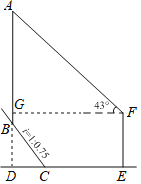
A.46.7mB.46.8mC.53.5mD.67.8m
【答案】B
【解析】
根据山坡的坡度i=1:0.75,可得![]() =
=![]() ,设BD=4x,CD=3x,然后利用勾股定理求得BD=4x=16m,CD=3x=12m;再利用矩形的性质求出FG=DE=46m,BG=DG﹣DB=4m,最后利用三角函数解直角三角形即可.
,设BD=4x,CD=3x,然后利用勾股定理求得BD=4x=16m,CD=3x=12m;再利用矩形的性质求出FG=DE=46m,BG=DG﹣DB=4m,最后利用三角函数解直角三角形即可.
解:如图,∵∠ADC=90°,i=1:0.75,即![]() =
=![]() ,
,
∴设BD=4x,CD=3x,则BC=![]() =5x=20m,
=5x=20m,
解得:x=4,
∴BD=4x=16m,CD=3x=12m,
易得四边形DEFG是矩形,
则EF=DG=20m,FG=DE=DC+CE=12+34=46(m),
∴BG=DG﹣DB=4m,
在Rt△AFG中,AG=FG·tan∠AFG=46·tan43°≈46×0.93=42.78(m),
∴AB=AG+BG=42.78+4≈46.8(m),
故选:B.

练习册系列答案
相关题目