Question

【题目】已知抛物线(m，n 为常数)．

（1）若抛物线的的对称轴为直线 x=1,且经过点（0，-1），求 m，n 的值；

（2）若抛物线上始终存在不重合的两点关于原点对称，求 n 的取值范围；

（3）在（1）的条件下，存在正实数 a，b( a＜b)，当 a≤x≤b 时，恰好有，请直接写出 a，b 的值．

Answer 1

【答案】（1）， （2） （3），

【解析】

（1）利用对称轴公式求出m的值，再用待定系数法求出n的值即可；

（2）设抛物线线上关于原点对称且不重合的两点坐标分别是和代入解析式可得，根据两点不重合可得；

（3）由（1）可知抛物线解析式为，再根据，当 a≤x≤b 时，恰好有，即可得，由二次函数的图象得到当时，；当时，，通过解方程求得a，b 的值．

（1）∵抛物线的的对称轴为直线

∴

解得

∴

将点（0，-1）代入中

解得；

（2）设抛物线线上关于原点对称且不重合的两点坐标分别是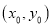和

代入解析式可得

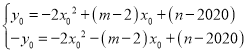
两式相加得

∴

∴；

∵当时，

解得

∴和重合

∴

∴

（3）由（1）可知抛物线解析式为

∴

∵，当 a≤x≤b 时，恰好有

∴，即

∴

∵抛物线的对称轴是，且开口向下

∴当a≤x≤b 时，y随x的增大而减小

∴当时，

当时，

∵

∴

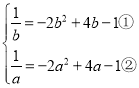
将①整理得

∵

∴

解得（舍去），

同理，由②得

∵

∴或

解得，（舍去），（舍去）

综上所述，，．