Question

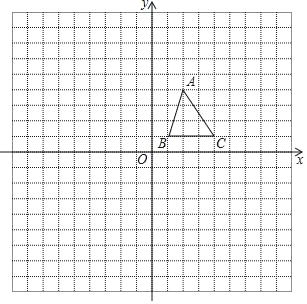
【题目】已知，在Rt△ABC中，∠ACB＝90°，D是BC边上一点，连接AD，分别以CD和AD为直角边作Rt△CDE和Rt△ADF，使∠DCE＝∠ADF＝90°，点E，F在BC下方，连接EF．

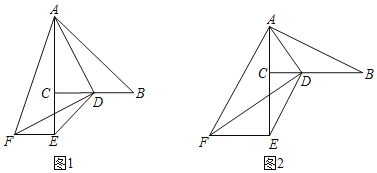
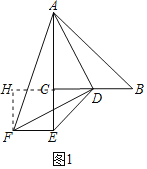
（1）如图1，当BC＝AC，CE＝CD，DF＝AD时，

求证：①∠CAD＝∠CDF，

②BD＝EF；

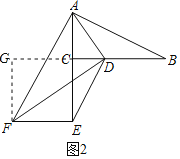
（2）如图2，当BC＝2AC，CE＝2CD，DF＝2AD时，猜想BD和EF之间的数量关系？并说明理由．

Answer 1

【答案】（1）①见解析；②见解析；（2）BD＝EF，理由见解析.

【解析】

（1）①根据同角的余角相等证明；

②作FH⊥BC交BC的延长线于H，证明△ACD≌△DHF，根据全等三角形的性质得到DH=AC，结合图形证明即可；

（2）作FG⊥BC交BC的延长线于G，证明△ACD∽△DGF，根据相似三角形的性质得到DG=2AC，证明结论．

（1）证明：①∵∠ACB＝90°，

∴∠CAD+∠ADC＝90°，

∵∠CDF+∠ADC＝90°，

∴∠CAD＝∠CDF；

②作FH⊥BC交BC的延长线于H，

则四边形FECH为矩形，

∴CH＝EF，

在△ACD和△DHF中，

，

，

，

，

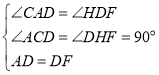，即，

；

（2），

理由如下：作交的延长线于，

则四边形为矩形，

，

，，

，

，即，GF＝2CD，

∵BC＝2AC，CE＝2CD，

∴BC＝DG，GF＝CE，

∴BD＝CG，

∵GF∥CE，GF＝CE，∠G＝90°，

∴四边形FECG为矩形，

∴CG＝EF，

∴BD＝EF．