题目内容
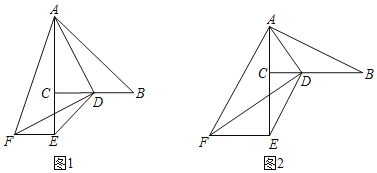
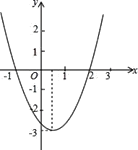
【题目】已知:点D、E、F分别是等边△ABC三边上的三等分点,AD、BE、CF两两相交于P、Q、R点,(如图所示),求△PQR的面积与△ABC面积的比值.
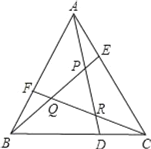
【答案】S△PQR:S△ABC=1:7.
【解析】
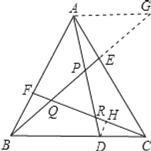
可作AG∥BC交BE延长线于点G,作DH∥AB交CF于点H,由平行线分线段成比例可得线段之间的比例关系,进而转化为三角形的面积关系,即可求解结论.
解:作AG∥BC交BE延长线于点G,作DH∥AB交CF于点H,
则得:
AG:BC=AE:EC=1:2,AG:BD=3:4,
又由于DH:BF=1:3,DH:AF=1:6,
所以DR:AR=1:6,DR:DA=1:7,
从而S△CDR=![]() S△BFC=
S△BFC=![]() S△ABC,
S△ABC,
同理可得S△BFQ= S△APE=![]() S△ABC,
S△ABC,
∵S△PQR=S△BCE(S△BCFS△BFQ)(S△ACDS△APES△CDR)=![]() S△ABC-(
S△ABC-(![]() S△ABC
S△ABC ![]() S△ABC)(
S△ABC)(![]() S△ABC
S△ABC ![]() S△ABC
S△ABC ![]() S△ABC)=
S△ABC)=![]() S△ABC
S△ABC
因此S△PQR:S△ABC=1:7.

练习册系列答案
相关题目
【题目】(9分)九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为![]() 元.
元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 元;②月销量是 件;(直接写出结果)
(2)设销售该运动服的月利润为![]() 元,那么售价为多少时,当月的利润最大,最大利润是多少?
元,那么售价为多少时,当月的利润最大,最大利润是多少?