题目内容
【题目】如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
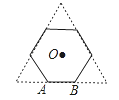
(1)求这个正六边形的边长.
(2)求这个正六边形的边心距.
(3)设这个正六边形的中心为O,一边为AB,则AB绕点O旋转一周所得的图形是怎样的?(作图表示出来)并求出这条线段AB划过的面积.
【答案】(1)正六边形的边长为2;(2)OD=![]() ;(3)线段AB划过的面积为πcm2 .
;(3)线段AB划过的面积为πcm2 .
【解析】
(1)根据题意和正六边形的性质求出正六边形的边长;
(2)求出正六边形的中心角,根据正弦的概念解答即可;
(3)根据题意画出图形,根据圆的面积公式计算即可.
(1)∵六边形DFABGE是正六边形,
∴∠EDF=∠DFA=∠FAB=∠ABG=∠BGE=∠GED=120°,DE=DF,
∴∠ADE=∠AED=60°,
∴△HDE是等边三角形,
∴HD=DE=HE,
同理:FK=KA=AF,
∴HD=DF=FK=2,
∴正六边形的边长为2 cm;
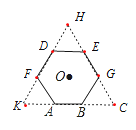
(2)解:连接OA,OB,过点O作ON⊥AB于点N,

∵∠AOB=![]() =60°,
=60°,
∴△OAB是等边三角形,
∴ON=OAsin60°=2×![]() cm;
cm;
(3)如图:
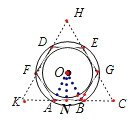
线段AB划过的轨迹是一个圆环,其面积=π×22﹣π×(![]() )2=πcm2 .
)2=πcm2 .

练习册系列答案
相关题目