题目内容
【题目】如图,已知AB、AC是⊙O的弦,AB、AC的长分别等于⊙O的内接正六边形和正五边形的边长.
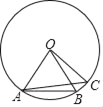
(1)试判断BC的长是否等于⊙O的内接正几边形的边长;
(2)如果⊙O的半径OA=6,求⊙O的内接正六边形的面积.
【答案】(1)BC的长等于⊙O的内接正30边形的边长,理由见解析;
(2)⊙O的内接正六边形的面积为![]() .
.
【解析】
(1)因为AB、AC的长分别等于⊙O的内接正六边形和正五边形的边长,所以∠AOB=60°,∠AOC=72°,即∠BOC=12°,即可得出BC的长等于⊙O的内接正30边形的边长;
(2)先算出△OAB的面积,即可得出⊙O的内接正六边形的面积.
解:(1)∵AB、AC是⊙O的弦,AB、AC的长分别等于⊙O的内接正六边形和正五边形的边长,
∴∠AOB=60°,∠AOC=72°,
∴∠BOC=12°,
∴n=360÷12=30,
∴BC的长等于⊙O的内接正30边形的边长;
(2)∵⊙O的半径OA=6,且△OAB为等边三角形,
∴⊙O的内接正六边形的面积为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目