题目内容
【题目】如图，点
为平面直角坐标系的原点，在矩形
中，两边
、
分别在
轴和
轴上，且点
满足：
．
（1）求点
的坐标（___，_____）；
（2）若过点的直线
与矩形的边交于点
，且将矩形的面积分为
两部分，
①求直线的解析式；
②在直线确定一点
，使得
的面积等于矩形的面积，求点的坐标；
（3）
在线段
上，
，
在坐标轴上，
为（2）中直线上一动点，若四点、、、构成平行四边形，直接写出的坐标．
【答案】（1）（
，-4）；（2）①y=
，②（
,
）或（0，4）；（3）（3
，0）或（，0）或（0，6）或（0，2）
【解析】
（1）根据非负数性质可求出a,b;
（2）①结合图，根据三角形面积关系求出P的坐标，用待定系数法求解；
②根据题意作图，可得Q的位置有两种情况：根据轴对称性质可得一种在y轴上；根据S△ACQ1=S梯形AOEQ1-S△AOC-S△CEQ1=S矩形ABCO可求出第二种情况；
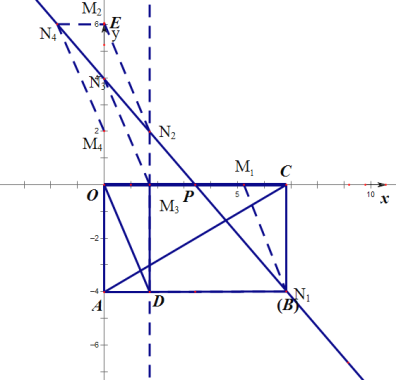
（3）根据平行四边形判定，过D作y轴的平行线与PB相交于N2，将OD沿AB平移至M1N1或沿y轴平移至M3N3或至M2N2可得到以OD为边的平行四边形；当N4E∥AD,且N4E=AD时，OD∥N4M4 ,ODN4=M4,也可得到以OD为边的平行四边形；分别可求出M的坐标．
解：（1）因为
所以
=0，
所以
，b=-4
所以B（，-4）
（2）①如图，由已知可得△PBC的面积是：
=
所以PC=
所以OP=OC-PC=
所以P（，0）
设直线BP的解析式是y=kx+b
则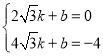
解得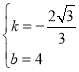
所以BP的解析式是y=
②如图，Q的位置有两种情况：
第一种：Q2位置
直线y=与y轴的交点是Q2（0，4）,
因为A（0，-4）
所以Q2，A关于x轴对称
所以三角形ACQ2的面积=2S△AOC=矩形ABCO的面积．
第二种：Q1位置
设Q1（
）
由S△ACQ1=S梯形AOEQ1-S△AOC-S△CEQ1=S矩形ABCO得
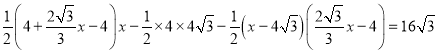
解得
所以
所以Q1（,）
所以Q的坐标是（,）或（0，4）
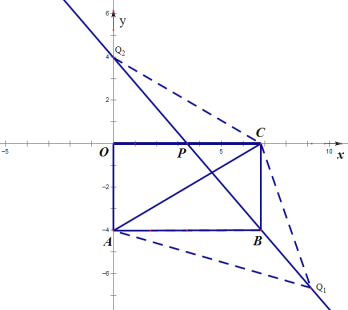
（3）如图，过D作y轴的平行线与PB相交于N2，将OD沿AB平移至M1N1或沿y轴平移至M3N3或至M2N2可得到以OD为边的平行四边形；当N4E∥AD,且N4E=AD时，OD∥N4M4 ,ODN4=M4,也可得到以OD为边的平行四边形；
因为AD=
所以 AD=
所以BD=3
所以M1（3，0），M3（，0）
N2（，2）
所以DN2=2+4=6
所以OM2=6
所以M2（0，6）
当N4E∥AD且N4E=AD=时，可得E（0，6），
当EM4=OA=4,即M4（0，2）时，可得△N4EM4≌△DAO（SAS）
此时，∠N4M4E=∠AOD
所以∠N4M4O=∠DOE
所以N4M4∥OD
此时可得到OD为边的平行四边形；
综合上述，M的坐标是：（3，0）或（，0）或（0，6）或（0，2）
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案【题目】近年来，由于土地沙化日渐加剧，沙尘暴频繁，严重影响国民生活．为了解某地区土地沙化情况，环保部门对该地区进行了连续四年跟踪观测，所记录的近似数据如下表：
观测时间 | 第1年 | 第2年 | 第3年 | 第4年 |
沙漠面积 | 90万亩 | 90.2万亩 | 90.4万亩 | 90.6万亩 |
（1）根据表中提供的信息，在不采取任何措施的情况下，试定出该地区沙漠面积y（万亩）与x（年数）之间的关系式（用含x的式子表示y），并计算到第20年时该地区的沙漠面积；
（2）为了防沙治沙，政府决定投入资金，鼓励农民植树种草，经测算，植树1亩需资金200元，种草1亩需资金100元．某组农民计划在一年内完成2400亩绿化任务．在实施中，由于实际情况所限，植树完成了计划的90%，种草超额完成了计划的20%，恰好完成了计划的绿化任务，那么所节余的资金还能植树多少亩？
