题目内容
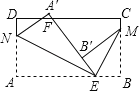
【题目】如图,点E,F在矩形的边AD,BC上,点B与点D关于直线EF对称.设点A关于直线EF的对称点为G.
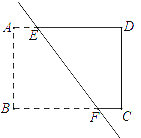
(1)画出四边形ABFE关于直线EF对称的图形;
(2)若∠FDC=16°,直接写出∠GEF的度数为 ;
(3)若BC=4,CD=3,写出求线段EF长的思路.
【答案】(1)见解析;(2)127°;(3)见解析.
【解析】
(1)直接利用轴对称图形的性质得出对应点位置进而得出答案;
(2)利用翻折变换的性质结合平行线的性质得出∠1度数进而得出答案;
(3)利用翻折变换的性质结合勾股定理得出答案.
(1)如图所示:
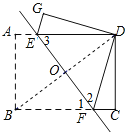
(2)∵∠FDC=16°,
∴∠DFC=74°,
由对称性得,∠1=∠2=![]()
∵AD∥BC,
∴∠AEF=∠GEF=180°-53°=127°;
故答案为:127°.
(3)思路:
a.连接BD交EF于点O.
b.在Rt△DFC中,设FC=x,则FD=4-x,由勾股定理,求得FD长;
c.Rt△BDC中,勾股可得BD=5,由点B与点D的对称性可得OD的长;
d.在Rt△DFO中,同理可求OF的长,可证EF=2OF,求得EF的长.

 阅读快车系列答案
阅读快车系列答案【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | …… |
月销量(件) | 200 | 180 | 160 | 140 | …… |
(1)已知该运动服的进价为每件60元,设售价为x元;
请用含有x的式子表示:
①销售该运动服每件的利润是 元;
②月销售量是 件;(直接写结果)
(2)设销售该运动服的月利润为y元,那么售价为多少元时,当月的利润最大?最大利润是多少?
【题目】我国每年的总用水主要包括四大方面:农业用水、工业用水、生活用水、其他用水. 2017年,我国农业用水量约![]() 亿
亿![]() (占总用水量的
(占总用水量的![]() ),工业用水量约为
),工业用水量约为![]() 亿
亿![]() ,生活用水量具体见下表.
,生活用水量具体见下表.
2019-2017年全国生活用水量表(单位:亿![]() )
)
年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
用水量 |
|
|
|
|
|
|
|
|
|
(1)2017年全国总用水量约为 亿![]() ,其他用水约为 亿
,其他用水约为 亿![]() .
.
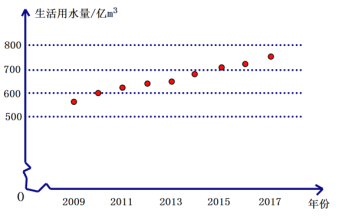
(2)根据“2019-2017年全国生活用水量表”,在平面直角坐标系中描出表中各对数值所对应的点(其中横坐标表示年份,纵坐标表示用水量)可发现,这些点近似的落在某条直线上.
①用靠近尽可能多点的直线来表示用水量的这种趋势,请在上图中画出这条直线;
②根据所画的直线,估计2018年全国生活用水量,并说明理由.