Question

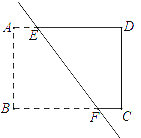
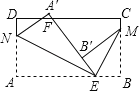
【题目】如图，长方形纸片ABCD，点E，F分别在边AB，CD上，连接EF，将∠BEF对折，点B落在直线EF上的点B'处，得折痕EM；将∠AEF对折，点A落在直线EF上的点A'处，得折痕EN，若∠DNA'的度数为α，请用含α的式子表示∠BME的度数．

Answer 1

【答案】α

【解析】

由矩形的性质得出∠A＝∠B＝90°，由翻折的性质可知∠ANE＝∠A′NE＝（180°﹣α）＝90°﹣α，∠AEN＝90°﹣∠ANE＝α，由翻折的性质可知∠AEN＝∠A′EN，∠BEM＝∠B′EM，则∠NEM＝∠A′EN+∠B′EM＝（∠AEA′+∠BEB′）＝90°，由翻折的性质可知∠MB′E＝∠B＝90°，由∠MEB′+∠A′EN＝∠B′ME+∠MEB′＝90°，得出∠B′ME＝∠A′EN，∠EMB＝∠EMB′，推出∠BME＝∠AEN＝α．

∵四边形ABCD是矩形，

∴∠A＝∠B＝90°，

∵∠DNA'＝α，

∴由翻折的性质可知：∠ANE＝∠A′NE＝（180°﹣α）＝90°﹣α，

∴∠AEN＝90°﹣∠ANE＝90°﹣90°+α＝α，

由翻折的性质可知：∠AEN＝∠A′EN，∠BEM＝∠B′EM，

∴∠NEM＝∠A′EN+∠B′EM＝（∠AEA′+∠BEB′）＝×180°＝90°，

由翻折的性质可知：∠MB′E＝∠B＝90°，

∴∠MEB′+∠A′EN＝∠B′ME+∠MEB′＝90°，

∴∠B′ME＝∠A′EN，

∴∠EMB＝∠EMB′，

∴∠BME＝∠AEN＝α．