题目内容
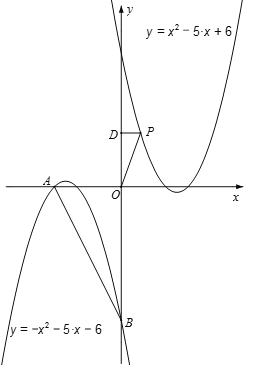
【题目】在平面直角坐标系中,已知抛物线L:![]() 经过点A(-3,0)和点B(0,-6),L关于原点O对称的抛物线为
经过点A(-3,0)和点B(0,-6),L关于原点O对称的抛物线为![]() .
.
(1)求抛物线L的表达式;
(2)点P在抛物线![]() 上,且位于第一象限,过点P作PD⊥y轴,垂足为D.若△POD与△AOB相似,求符合条件的点P的坐标.
上,且位于第一象限,过点P作PD⊥y轴,垂足为D.若△POD与△AOB相似,求符合条件的点P的坐标.
【答案】(1) y=-x2-5x-6;(2)符合条件的点P的坐标为(1,2)或(6,12)或(![]() ,
,![]() )或(4,2)。
)或(4,2)。
【解析】
(1)利用待定系数法进行求解即可得;
(2)由关于原点对称的点的坐标特征可知点A(-3,0)、B(0,-6)在L′上的对应点分别为A′(3,0)、B′(0,6),利用待定系数法求得抛物线L′的表达式为y=x2-5x+6,设P(m,m2-5m+6)(m>0),根据PD⊥y轴,可得点D的坐标为(0,m2-5m+6),可得PD=m,OD=m2-5m+6,再由Rt△POD与Rt△AOB相似,分Rt△PDO∽Rt△AOB或Rt△ODP∽Rt△AOB两种情况,根据相似三角形的性质分别进行求解即可得.
(1)由题意,得 ,
,
解得:![]() ,
,
∴L:y=-x2-5x-6;
(2)∵抛物线L关于原点O对称的抛物线为![]() ,
,
∴点A(-3,0)、B(0,-6)在L′上的对应点分别为A′(3,0)、B′(0,6),
∴设抛物线L′的表达式y=x2+bx+6,
将A′(3,0)代入y=x2+bx+6,得b=-5,
∴抛物线L′的表达式为y=x2-5x+6,
∵A(-3,0),B(0,-6),
∴AO=3,OB=6,
设P(m,m2-5m+6)(m>0),
∵PD⊥y轴,
∴点D的坐标为(0,m2-5m+6),
∵PD=m,OD=m2-5m+6,
∵Rt△PDO与Rt△AOB相似,
∴有Rt△PDO∽Rt△AOB或Rt△ODP∽Rt△AOB两种情况,
①当Rt△PDO∽Rt△AOB时,则![]() ,即
,即![]() ,
,
解得m1=1,m2=6,
∴P1(1,2),P2(6,12);
②当Rt△ODP∽Rt△AOB时,则![]() ,即
,即![]() ,
,
解得m3=![]() ,m4=4,
,m4=4,
∴P3(![]() ,
,![]() ),P4(4,2),
),P4(4,2),
∵P1、P2、P3、P4均在第一象限,
∴符合条件的点P的坐标为(1,2)或(6,12)或(![]() ,
,![]() )或(4,2).
)或(4,2).