题目内容
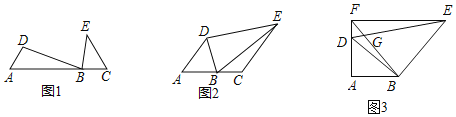
【题目】如图,在等腰直角三角形△ABC中,AC=6![]() ,∠C=90°,∠DCE=45°,AD=3,则BE的长为_____________________
,∠C=90°,∠DCE=45°,AD=3,则BE的长为_____________________
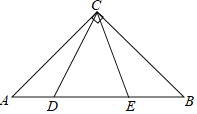
【答案】4
【解析】
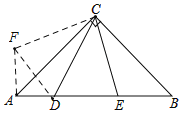
将△BCE绕点C逆时针旋转90°得到△ACF,连接DF,由旋转的性质可得AF=BE,CF=EC,∠FAC=∠ABC=45°=∠CAB,∠ACF=∠BCE,即可证△FCD≌△ECD,可得DE=DF,根据勾股定理可求BE的长度.
如图,将△BCE绕点C逆时针旋转90°得到△ACF,连接DF,
∵∠ACB=90°,AC=BC=6![]() ,
,
∴AB=12,∠CAB=∠ABC=45°,
∵AD=3,
∴BD=9=DE+BE,
∵将△BCE绕点C逆时针旋转90°得到△ACF
∴△AFC≌△BEC
∴AF=BE,CF=CE,∠FAC=∠ABC=45°=∠CAB,∠ACF=∠BCE,
∴∠FAD=90°
∵∠DCE=45°,∠ACB=90°,
∴∠ACD+∠BCE=45°,
∴∠ACD+∠FCA=45°=∠DCE,且CF=BC,CD=CD,
∴△FCD≌△ECD(SAS)
∴DE=DF,
在Rt△ADF中,DF![]() =AD
=AD![]() +AF
+AF![]() ,
,
∴(9-BE)![]() =9+BE
=9+BE![]() ,
,
∴BE=4
故答案为:4

练习册系列答案
相关题目