Question

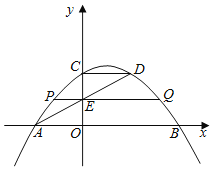
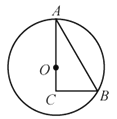
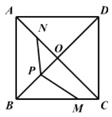
【题目】如图，在正方形ABCD中，AB=8，AC与BD交于点O，N是AO的中点，点M在BC边上，且BM=6. P为对角线BD上一点，则PM—PN的最大值为___.

Answer 1

【答案】2.

【解析】

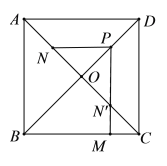
如图所示，以BD为对称轴作N的对称点，连接，根据对称性质可知，，由此可得，当三点共线时，取“=”，此时即PM—PN的值最大，由正方形的性质求出AC的长，继而可得，，再证明，可得PM∥AB∥CD，∠90°，判断出△为等腰直角三角形，求得长即可得答案.

如图所示，以BD为对称轴作N的对称点，连接，根据对称性质可知，，∴，当三点共线时，取“=”，

∵正方形边长为8，

∴AC=AB=，

∵O为AC中点，

∴AO=OC=，

∵N为OA中点，

∴ON=，

∴，

∴，

∵BM=6，

∴CM=AB-BM=8-6=2，

∴，

∴PM∥AB∥CD，∠90°，

∵∠=45°，

∴△为等腰直角三角形，

∴CM==2，

故答案为：2.