题目内容
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() ,垂足
,垂足![]() 在线段
在线段![]() 上,连接
上,连接![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,则
,则![]() °.
°.
【答案】(1)见解析;(2)105.
【解析】
(1)分别延长![]() ,
,![]() 交于点
交于点![]() ,先证明
,先证明![]() 得BF=FG,再证明
得BF=FG,再证明![]() 为
为![]() 的中线即可得到结论;
的中线即可得到结论;
(2)设∠FEB=x,则∠FBE=x,求得∠EFB=180°-2x,∠AFB=90°-x,证明∠AFE=3∠DEF即可求得结论.
(1) 证明:如图,分别延长![]() ,
,![]() 交于点
交于点![]() ,
,
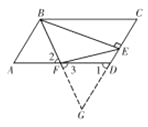
∵四边形![]() 是平行四边形.
是平行四边形.
∴![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
在![]() 与
与![]() 中,
中,
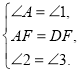
∴![]()
∴![]() .
.
即![]() 为
为![]() 的中线.
的中线.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
(2) ∵![]()
∴∠FEB=∠FBE
设∠FEB=x,则∠FBE=x,
∵AB//CD, BE⊥CD
∴∠ABE=90゜
∴∠ABF=∠AFB=90°-x,
∴∠EFB=180°-2x,
∴∠EFA=90°-x+180°-2x=270°-3x,
∵∠DEF=90°-x,且![]()
∴∠AFE=3∠DEF=105°.
故答案为:105°.

练习册系列答案
相关题目