题目内容
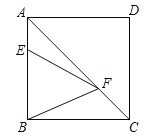
【题目】如图所示，O是矩形ABCD的对角线的交点，DE∥AC，CE∥BD．
（1）求证：OE⊥DC．
（2）若∠AOD＝120°，DE＝2，求矩形ABCD的面积．
【答案】（1）证明见解析（2）4
【解析】
(1) 要证OE⊥DC，可先证四边形OCED是菱形．由DE∥AC，CE∥BD，可得四边形OCED是平行四边形；又因为ABCD是矩形，所以OC=OD．有一组邻边相等的平行四边形是菱形．
(2)由(1) 得出△ODC是等边三角形,所以 DC=OD=OC=2 ,由四边形ABCD是矩形,得到AC=2CO=4, 在Rt△ADC中，由勾股定理得AD=2 ，再利用矩形面积公式即可解答.
(1)证明：
∵DE∥AC,CE∥BD
∴DE∥OC,CE∥OD
∴四边形ODEC是平行四边形
∵四边形ODEC是矩形
∴OD=OC
∴四边形ODEC是菱形
∴OE⊥DC
(2)解：∵DE=2,由（1）知，四边形ODEC是菱形
∴OD=OC=DE=2
∵∠AOD=120°
∴∠DOC=60°
∴△ODC是等边三角形
∴DC=OD=OC=2
∵四边形ABCD是矩形
∴AC=2CO=4
在Rt△ADC中，由勾股定理得AD=2
∴S矩形ABCD=2×2=4
练习册系列答案
相关题目
【题目】研究“掷一枚图钉，钉尖朝上”的概率，两个小组用同一个图钉做试验进行比较，他们的统计数据如下：
掷图钉的次数 | 50 | 100 | 200 | 300 | 400 |
钉尖朝上 的次数 | |||||
第一小组 | 23 | 39 | 79 | 121 | 160 |
第二小组 | 24 | 41 | 81 | 124 | 164 |
(1)请你估计第一小组和第二小组所得的概率分别是多少？
(2)你认为哪一个小组的结果更准确？为什么？
