题目内容
【题目】如图,直线 
∥ 
∥ 
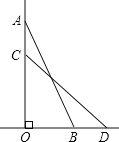
，且 与 的距离为1， 与 的距离为2,等腰 △ABC的顶点分别在直线 ， ， 上，AB=AC，∠BAC=120° ，则等腰三角形的底边长为。
【答案】6 
， 2 , 2 
, 2 
.
【解析】解 ：此题分四种情况 ：①如图1中,作BF⊥l1于F交l3于H,取BC的中点E,过点E作l4∥l3 ， 交FH于点M,连接AE.取AB的中点O，连接OF、OE.
∵AB=AC，BE=EC， ∠BAC=120°，
∴AE⊥BC,∠BAE=60，
∵BF⊥AF，
∴∠AFB=∠AEB=90，
∴OA=OB=OF=OE，
∴A、F. B. E四点共圆，
∴∠BFE=∠BAE=60，
∵l1∥l2∥l3∥l4 ， BE=EC，
∴BF=BM=MH=1，
在Rt△EFM中,EM=FMtan60=2 ，
在Rt△BEM中,由勾股定理得：BE=
∴BC=2BE=2
②如图2中,作BF⊥l3于F交l2于G,取BC的中点E,过点E作l 4∥l1交BF于H ，连接EF,AE,
.
同理可证B. F. A. E四点共圆，
∴∠BFE=∠BAE=60，
∵BE=EC,l1∥l4∥l2 ，
∴BH=HG=
，
在Rt△EHF中,HE=FHtan60=
在Rt△BEH中,由勾股定理得：BE=
∴BC=2BE=2
③如图3中,在直线l2取一点A,作AB⊥l2交l3于B,作∠CAB=120,作CE⊥l2于E. 过点A作AD⊥BC于点D, 
∵∠CAE=∠CAB∠EAB=12090=30 ，
∴在Rt△ACE中，AC=2EC=2，
∵AB=2，
∴AC=AB，
∴△ABC满足条件，
∴AB=2，
∵△ABC中 ，∠CAB=120 ， AB=AC,AD⊥BC
∴∠ACB=30° ,BC=2CD
∴BC=2CD=2；
④如图所示 ：过点A作AD⊥BC与点D ;∵∵
∵AD⊥BC,AB=AC,∠CAB=120
∴BC=2DB,∠ADB=90°,∠BAD=60°,AD=3,
∴BD=AD·tan60°=3,
∴BC=6;
综上所述,等腰三角形的底边长为
， 
,
,
.分四种情形讨论：①如图1中，作BF⊥l1于F交l3于H，取BC的中点E，过点E作l4∥l3 ， 连接AE．取AB的中点O，连接OF、OE．首先证明A、F、B、E四点共圆，推出∠BFE=∠BAE=60°，在Rt△EMF中，求出EM，在Rt△BME中求出BE即可解决问题．②如图2中，作BF⊥l3于F交l2于G，取BC的中点E，过点E作l 4∥l1交BF于H．解法类似①．③如图3中，在直线l2取一点A，作AB⊥l2交l3于B，作∠CAB=120°，作CE⊥l2于E． 过点A作AD⊥BC于点D, 只要证明△ABC是等腰三角形即可，然后根据含30°直角三角形的边之间的关系得出AD，进而利用勾股定理求出UCD，从而得出答案；④过点A作AD⊥BC与点D ，根据等腰三角形的三线合一得出BC=2DB，根据平行线间的距离得出AD=3,根据正切函数的定义得出BD的长度，进而得出BC的长度，综上所述得出本题答案。
