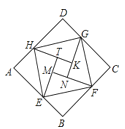
[题目]如图是由“赵爽弦图变化得到的.它由八个全等的直角三角形拼接而成.记图中正方形ABCD.正方形EFGH.正方形MNKT的面积分别为,若.则的值是．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为,若，则的值是_______．

【答案】12

【解析】

设8个全等的直角三角形的每个三角形面积为x，中间的正方形MNKT面积为y，则正方形ABCD的面积为8x+y，正方形EFGH的面积为4x+y，正方形MNKT面积为y=，

再利用，可知4x+y=12.

设8个全等的直角三角形的每个三角形面积为x，中间的正方形MNKT面积为y，则正方形ABCD的面积为8x+y，正方形EFGH的面积为4x+y，正方形MNKT面积为y=，

∵，

∴（8x+y）+y=24，

则2（4x+y）=24，即4x+y=12，故=12.

练习册系列答案

创新成功学习快乐暑假云南科技出版社系列答案

相关题目

【题目】如图，抛物线C1：y=x2+bx+c经过原点，与x轴的另一个交点为（2，0），将抛物线C1向右平移m（m＞0）个单位得到抛物线C2 ， C2交x轴于A，B两点（点A在点B的左边），交y轴于点C．
（1）求抛物线C1的解析式及顶点坐标；
（2）以AC为斜边向上作等腰直角三角形ACD，当点D落在抛物线C2的对称轴上时，求抛物线C2的解析式；
（3）若抛物线C2的对称轴存在点P，使△ PAC为等边三角形，求m的值．

【题目】某学校在疫情期间利用网络组织了一次防“新冠病毒”知识竞赛，评出特等奖10人，优秀奖20人．学校决定给所有获奖学生各发一份奖品，同一等次的奖品相同．

（1）（列方程组解应用题）若特等奖和优秀奖的奖品分别是口罩和温度计，口罩单价的2倍与温度计单价的3倍相等，购买这两种奖品一共花费700元，求口罩和温度计的单价各是多少元？

（2）（利用不等式或不等式组解应用题）若两种奖品的单价都是整数，且要求特等奖单价比优秀奖单价多20元．在总费用不少于440而少于500元的前提下，购买这两种奖品时它们的单价有几种情况，请分别求出每种情况特等奖和优秀奖奖品的单价．

【题目】夏季空调销售供不应求，某空调厂接到一份紧急订单，要求在10天内（含10天）完成任务，为提高生产效率，工厂加班加点，接到任务的第一天就生产了空调42台，以后每天生产的空调都比前一天多2台，由于机器损耗等原因，当日生产的空调数量达到50台后，每多生产一台，当天生产的所有空调，平均每台成本就增加20元．
（1）设第x天生产空调y台，直接写出y与x之间的函数解析式，并写出自变量x的取值范围．
（2）若每台空调的成本价（日生产量不超过50台时）为2000元，订购价格为每台2920元，设第x天的利润为W元，试求W与x之间的函数解析式，并求工厂哪一天获得的利润最大，最大利润是多少．

【题目】如图，在中，，点是的中点，过点作，垂足在线段上，连接，．