Question

【题目】重庆八中某数学兴趣小组同学探究函数的图象与性质，根据学习函数的经验，该小组进行了系列探究．

下表给出了自变量与函数的一些对应值：

	…	-3	-2	-1	0	1	2	3	…
	…	2	3	4			1		…

（1）补全表格： ， ；

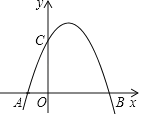
（2）在如图所示的面直角坐标系中，补全函数的图象并写出该函数的一条性质：

____________________________________________________________________________；

（3）若函数，直接写出不等式的解集．

Answer 1

【答案】（1）2， ；（2）当时，函数取得最大值4（或当时，随的增大而增大，当时，随的增大而减小，答案不唯一）；（3）或．

【解析】

（1）将和代入即可求出和的值；

（2）根据表格数据，描点作图即可，从函数最值，增减性方面写出一条性质即可；

（3）作出的图象，并求出与的交点横坐标，结合图象即可得出答案．

（1）∵0和1都大于-1

∴将和分别代入得

，，

故答案为：2， ；

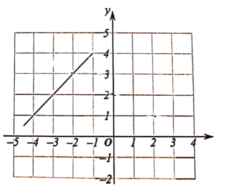
（2）如图所示：

性质：当时，函数取得最大值4，

或当时，随的增大而增大，当时，随的增大而减小．（答案不唯一）

（3）如图，作出的图象，

令，解得，

令，解得或2，

则与交点横坐标分别为-2，0，2，

由图像可得不等式的解集为或.