题目内容
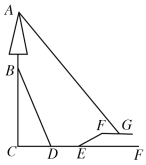
【题目】我校数学社团学生小明想测量学校对面斜坡
上的信号树
的高度，已知的坡度为
，且的长度为65米，小明从坡底
处沿直线走到学校大台阶底部
处，
长为20米，他沿着与水平地面成
夹角的大台阶行走20米到达平台
处，又向前走了13米到达平台上的旗杆
处，此时他仰望信号树的顶部
，测得仰角为
，则信号树的高度约为（ ）（小明的身高忽略不计）
（参考数据：
，
，
，
，
）
A.45米B.30米C.35米D.40米
【答案】D
【解析】
延长GF交AC于点M，过F作FH⊥CF于点H，首先由BD的坡度和长度求出BC与CD，然后在Rt△EFH中，利用30度的三角函数值求出FH与EH，结合已知条件可得到MG，再在△AMG中求出AM，减去BM即为AB的高度．
如图，延长GF交AC于点M，过F作FH⊥CF于点H，
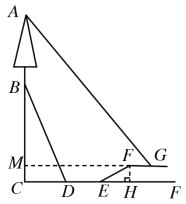
BD的坡度为
，即
设
米，
米，
由勾股定理得
，即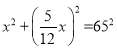
解得
则BC=60米，CD=
米
在Rt△EFH中，∠FEH=30°
∴EH=
EF=
米，EH=
FH=
米
∴MG=MF+FG=CD+DE+EH+FG=25+20++13=
米
在Rt△AMG中，∠AGM=50°，
∴AM=
米
又∵BM=BC-MC=BC-FH=60-10=50米
∴AB=AM-BM=
米
故选：D．
阅读快车系列答案
【题目】重庆八中某数学兴趣小组同学探究函数
的图象与性质，根据学习函数的经验，该小组进行了系列探究．
下表给出了自变量
与函数
的一些对应值：
| … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| … | 2 | 3 | 4 |
|
| 1 |
| … |
（1）补全表格：
，
；
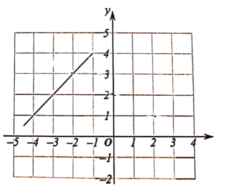
（2）在如图所示的面直角坐标系中，补全函数的图象并写出该函数的一条性质：
____________________________________________________________________________；
（3）若函数
，直接写出不等式
的解集．
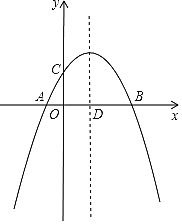
【题目】二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论：（1）ac＜0；
（2）抛物线顶点坐标为（1，5）；
（3）3是方程ax2+（b﹣1）x+c=0的一个根；
（4）当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0．其中正确的序号为___________________.
