题目内容
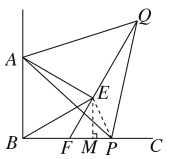
【题目】如图,∠ABC=90°, P为射线BC上任意一点(点P和点B不重合),分别以AB,AP为边在∠ABC内部作等边△ABE和等边△APQ, 连结QE并延长交BP于点F, 若FQ=6, AB=2![]() ,则BP=__________
,则BP=__________
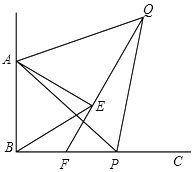
【答案】4
【解析】
连接EP,过点E作EM⊥BC,由题意可得△AQE≌△ABP,可得QE=BP,∠AEQ=∠ABC=90,可求∠EBF=∠BEF=30°,根据勾股定理可求BE=2EM=![]() ,BM=
,BM=![]() EM,EF=BF=2FM,EM=
EM,EF=BF=2FM,EM=![]() FM,可求BF=EF=2,EM=2
FM,可求BF=EF=2,EM=2![]() ,FM=1,由QF=6,EF=2,可得BP=EQ=4.
,FM=1,由QF=6,EF=2,可得BP=EQ=4.
如图,连接EP,过点E作EM⊥BC
∵△AEB,△APQ是等边三角形
∴AB=AE=BE=![]() ,AQ=AP,∠ABE=∠BAE=∠QAP=60°=∠AEB
,AQ=AP,∠ABE=∠BAE=∠QAP=60°=∠AEB
∴∠BAP=∠QAE
在△ABP和△QAE中,
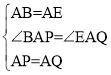
∴△ABP≌△QAE(SAS)
∴QE=BP,∠AEQ=∠ABP=90°
∵∠AEQ=∠ABC=90°,∠ABE=∠AEB=60°
∴∠BEF=∠EBF=30°
∴BF=EF,∠EFM=60°
∵EM⊥BC
∴∠FEM=30°
∴EF=2FM=BF,EM=![]() FM
FM
∵∠EBM=30°,EM⊥BC
∴BE=2EM,BM=![]() EM
EM
∵EB=2![]()
∴EM=![]() ,BM=3
,BM=3
∵BF+FM=BM
∴FM=1,BF=EF=2
∵QF=EQ+EF
∴EQ=62=4
∴BP=EQ=4
故答案为:4.

练习册系列答案
相关题目