题目内容
【题目】如图,网格中每个小正方形的边长为1,点B、C的坐标分别为(-1, 3), (0, 1).
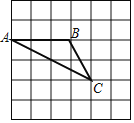
(1)建立符合条件的直角坐标系(要求标出x轴,y轴和原点),并写出点A的坐标
(2)线段AB上任意一点的坐标可以表示为
(3)在y轴上找到一点P,使得S△ABP = 3S△ABC,求出点P的坐标.
【答案】(1)见解析,A(-4,3);(2)(x,3)(-4≤x≤-1);(3)P(0,9)或P(0,-3)
【解析】
(1)将C(0,1)向下平移1格即可得到原点位置,作出坐标系,再根据A的位置写出坐标;
(2)AB∥x轴,纵坐标都为3,横坐标在-4到-1之间,据此可解答;
(3)易得S△ABC=3,可求出S△ABP=9,设P点坐标为(0,m),以AB为底边,根据面积公式列方程求解.
解:(1)如图所示,点A坐标为(-4,3);
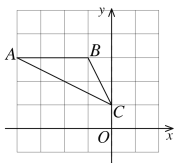
(2)∵A(-4,3),B(-1,3)
∴线段AB上任意一点的坐标可表示为(x,3)(-4≤x≤-1).
(3)由图可得S△ABP=3S△ABC=![]() ,
,
P点坐标为(0,m),则![]()
解得![]() 或9
或9
所以P点坐标为(0,9)或(0,-3).

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目