ЬтФПФкШн
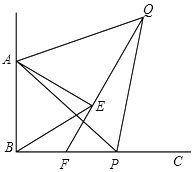
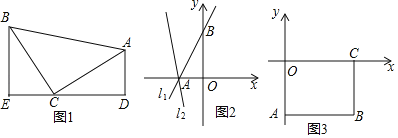
ЁОЬтФПЁПЃЈФЃаЭНЈСЂЃЉЃЈ1ЃЉШчЭМ1ЃЌЕШбќжБНЧШ§НЧаЮABCжаЃЌЁЯACBЃН90ЁуЃЌCBЃНCAЃЌжБЯпEDОЙ§ЕуCЃЌЙ§AзїADЁЭEDгкЕуDЃЌЙ§BзїBEЁЭEDгкЕуEЃЌЧѓжЄЃКЁїBECЁеЁїCDAЃЎ
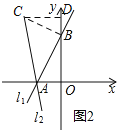
ЃЈФЃаЭгІгУЃЉЃЈ2ЃЉЂйвбжЊжБЯпl1ЃКyЃН![]() x+3гызјБъжсНЛгкЕуAЁЂBЃЌНЋжБЯпl1ШЦЕуAФцЪБеыа§зЊ45oжСжБЯпl2ЃЌШчЭМ2ЃЌЧѓжБЯпl2ЕФКЏЪ§БэДяЪНЃЛ
x+3гызјБъжсНЛгкЕуAЁЂBЃЌНЋжБЯпl1ШЦЕуAФцЪБеыа§зЊ45oжСжБЯпl2ЃЌШчЭМ2ЃЌЧѓжБЯпl2ЕФКЏЪ§БэДяЪНЃЛ
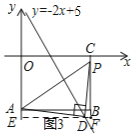
ЂкШчЭМ3ЃЌГЄЗНаЮABCOЃЌOЮЊзјБъдЕуЃЌЕуBЕФзјБъЮЊЃЈ8ЃЌЉ6ЃЉЃЌЕуAЁЂCЗжБ№дкзјБъжсЩЯЃЌЕуPЪЧЯпЖЮBCЩЯЕФЖЏЕуЃЌШєЁїAPDЪЧвдЕуDЮЊжБНЧЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃЌЕБЕуDдкжБЯпyЃНЉ2x+5ЩЯЪБЃЌжБНгаДГіЕуDЕФзјБъЃЌВЂаДГіећИідЫЖЏЙ§ГЬжаЕуDЕФзнзјБъnЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉЂйyЃНЉ5xЉ10ЃЛЂкDЃЈ3ЃЌЉ1ЃЉЛђ![]() ЃЌЉ10ЁмnЁмЉ7ЛђЉ2ЁмnЁм1ЃЎ
ЃЌЉ10ЁмnЁмЉ7ЛђЉ2ЁмnЁм1ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЁїABCЮЊЕШбќжБНЧШ§НЧаЮЃЌADЁЭEDЃЌBEЁЭEDЃЌПЩХаЖЈЁїACDЁеЁїCBEЃЛ
ЃЈ2ЃЉЂйЙ§ЕуBзїBCЁЭABЃЌНЛl2гкCЃЌЙ§CзїCDЁЭyжсгкDЃЌИљОнЁїCBDЁеЁїBAOЃЌЕУГіBD=AO=2ЃЌCD=OB=3ЃЌЧѓЕУCЃЈ-3ЃЌ5ЃЉЃЌзюКѓдЫгУД§ЖЈЯЕЪ§ЗЈЧѓжБЯпl2ЕФКЏЪ§БэДяЪНЃЛ
ЂкИљОнЁїAPDЪЧвдЕуDЮЊжБНЧЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃЌЕБЕуDЪЧжБЯпy=-2x+5ЩЯЕФЖЏЕуЧвдкЕкЫФЯѓЯоЪБЃЌЗжСНжжЧщПіЃКЕБЕуDдкОиаЮAOCBЕФФкВПЪБЃЌЕБЕуDдкОиаЮAOCBЕФЭтВПЪБЃЌЩшDЃЈxЃЌ-2x+5ЃЉЃЌЗжБ№ИљОнЁїADEЁеЁїDPFЃЌЕУГіAE=DFЃЌОнДЫСаГіЗНГЬНјааЧѓНтМДПЩЃЎЗжСНжжЧщаЮЧѓГіnЕФЗЖЮЇМДПЩЃЛ
НтЃКЃЈ1ЃЉжЄУїЃКШчЭМ1ЃЌЁпЁїABCЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЁрCBЃНCAЃЌЁЯACD+ЁЯBCEЃН90ЁуЃЌ
гжЁпADЁЭEDЃЌBEЁЭEDЃЌ
ЁрЁЯDЃНЁЯEЃН90ЁуЃЌЁЯEBC+ЁЯBCEЃН90ЁуЃЌ
ЁрЁЯACDЃНЁЯEBCЃЌ
дкЁїACDгыЁїCBEжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїACDЁеЁїCBEЃЈAASЃЉЃЛ
ЃЈ2ЃЉЂйШчЭМ2ЃЌЙ§ЕуBзїBCЁЭABЃЌНЛl2гкCЃЌЙ§CзїCDЁЭyжсгкDЃЌ
ЁпЁЯBACЃН45ЁуЃЌ
ЁрЁїABCЮЊЕШбќжБНЧШ§НЧаЮЃЌ
гЩЃЈ1ЃЉПЩжЊЃКЁїCBDЁеЁїBAOЃЌ
ЁрBDЃНAOЃЌCDЃНOBЃЌ
ЁпжБЯпl1ЃКyЃН![]() x+3жаЃЌШєyЃН0ЃЌдђxЃНЉ2ЃЛШєxЃН0ЃЌдђyЃН3ЃЌ
x+3жаЃЌШєyЃН0ЃЌдђxЃНЉ2ЃЛШєxЃН0ЃЌдђyЃН3ЃЌ
ЁрAЃЈЉ2ЃЌ0ЃЉЃЌBЃЈ0ЃЌ3ЃЉЃЌ
ЁрBDЃНAOЃН2ЃЌCDЃНOBЃН3ЃЌ
ЁрODЃН2+3ЃН5ЃЌ
ЁрCЃЈЉ3ЃЌ5ЃЉЃЌ
Щшl2ЕФНтЮіЪНЮЊyЃНkx+bЃЌдђ
![]() ЃЌ
ЃЌ
НтЕУ ![]() ЃЌ
ЃЌ
Ёрl2ЕФНтЮіЪНЃКyЃНЉ5xЉ10ЃЛ
ЂкЕБЕуDЪЧжБЯпyЃНЉ2x+5ЩЯЕФЖЏЕуЧвдкЕкЫФЯѓЯоЪБЃЌЗжСНжжЧщПіЃК
ЕБЕуDдкОиаЮAOCBЕФФкВПЪБЃЌШчЭМжаЃЌЙ§DзїxжсЕФЦНааЯпEFЃЌНЛжБЯпOAгкEЃЌНЛжБЯпBCгкFЃЌ
ЩшDЃЈxЃЌЉ2x+5ЃЉЃЌдђOEЃН2xЉ5ЃЌAEЃН6ЉЃЈ2xЉ5ЃЉЃН11Љ2xЃЌDFЃНEFЉDEЃН8ЉxЃЌ
гЩЃЈ1ЃЉПЩЕУЃЌЁїADEЁеЁїDPFЃЌдђDFЃНAEЃЌ
МДЃК11Љ2xЃН8ЉxЃЌ
НтЕУxЃН3ЃЌ
ЁрЉ2x+5ЃНЉ1ЃЌ
ЁрDЃЈ3ЃЌЉ1ЃЉЃЌ
ДЫЪБЃЌPFЃНEDЃН3ЃЌCPЃН4ЃМCBЃЌЗћКЯЬтвтЃЛ
ЕБЕуDдкОиаЮAOCBЕФЭтВПЪБЃЌШчЭМжаЃЌЙ§DзїxжсЕФЦНааЯпEFЃЌНЛжБЯпOAгкEЃЌНЛжБЯпBCгкFЃЌ
ЩшDЃЈxЃЌЉ2x+5ЃЉЃЌдђOEЃН2xЉ5ЃЌAEЃНOEЉOAЃН2xЉ5Љ6ЃН2xЉ11ЃЌDFЃНEFЉDEЃН8ЉxЃЌ
ЭЌРэПЩЕУЃКЁїADEЁеЁїDPFЃЌдђAEЃНDFЃЌ
МДЃК2xЉ11ЃН8ЉxЃЌ
НтЕУx=![]() ЃЌ
ЃЌ
Ёр-2x+5=-![]() ЃЌ
ЃЌ
ЁрDЃЈ ![]() ЃЌ-
ЃЌ-![]() ЃЉЃЌ
ЃЉЃЌ
ДЫЪБЃЌED=PF=![]() ЃЌPBЃМ6ЃЌЗћКЯЬтвтЃЎ
ЃЌPBЃМ6ЃЌЗћКЯЬтвтЃЎ
ЙЪТњзуЬѕМўЕФЕуDЃЈ3ЃЌ-1ЃЉЛђЃЈ![]() ЃЉЃЌ
ЃЉЃЌ
ЂйЕБЕуDдкAPЯТЗНЪБЃЌЕуPгыBжиКЯЪБЃЌDЃЈ4ЃЌЉ10ЃЉЃЛЕуPгыCжиКЯЪБЃЌDЃЈ7ЃЌЉ7ЃЉЃЌ
ЁрЉ10ЁмnЁмЉ7ЃЎ
ЂкЕБЕуDдкAPЩЯЗНЪБЃЌЕуPгыBжиКЯЪБЃЌDЃЈ4ЃЌЉ2ЃЉЃЛЕуPгыCжиКЯЪБЃЌDЃЈ1ЃЌ1ЃЉЃЌ
ЁрЉ2ЁмnЁм1ЃЎ
злЩЯЫљЪіЃЌЉ10ЁмnЁмЉ7ЛђЉ2ЁмnЁм1ЃЎ